写在前面
- 昨天, 我们学习了SVM中的软间隔与正则化; 今天, 我们继续学习SVM中的支持向量回归.
支持向量回归
- 现在我们来考虑回归问题. 给定训练样本
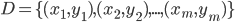 ,
, 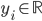 , 希望学得一个回归模型, 使得
, 希望学得一个回归模型, 使得 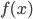 与
与 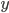 尽可能接近,
尽可能接近, 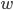 和
和  是待确定的模型参数.
是待确定的模型参数. - 对样本
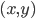 , 传统回归模型通常直接基于模型输出
, 传统回归模型通常直接基于模型输出 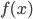 与真实输出
与真实输出 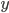 之间的差别来计算损失, 当且仅当
之间的差别来计算损失, 当且仅当 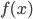 与
与 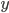 完全相同时, 损失才为零. 与此不同, 支持向量回归(Support Vector Regression, 简称SVR)假设我们能容忍
完全相同时, 损失才为零. 与此不同, 支持向量回归(Support Vector Regression, 简称SVR)假设我们能容忍 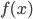 与
与 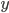 之间最多有
之间最多有 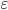 的偏差, 即仅当
的偏差, 即仅当 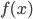 与
与 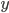 之间的差别绝对值大于
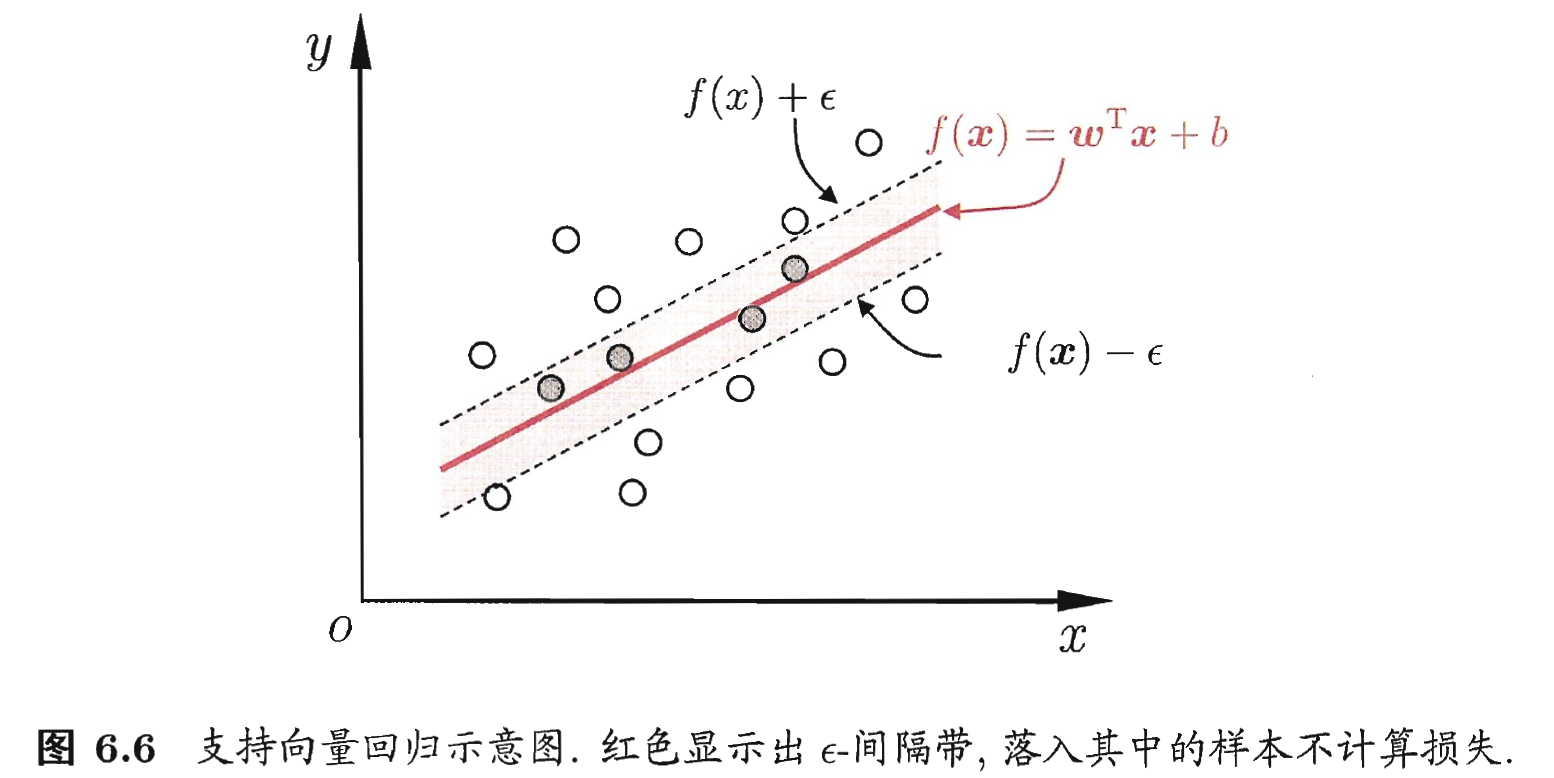
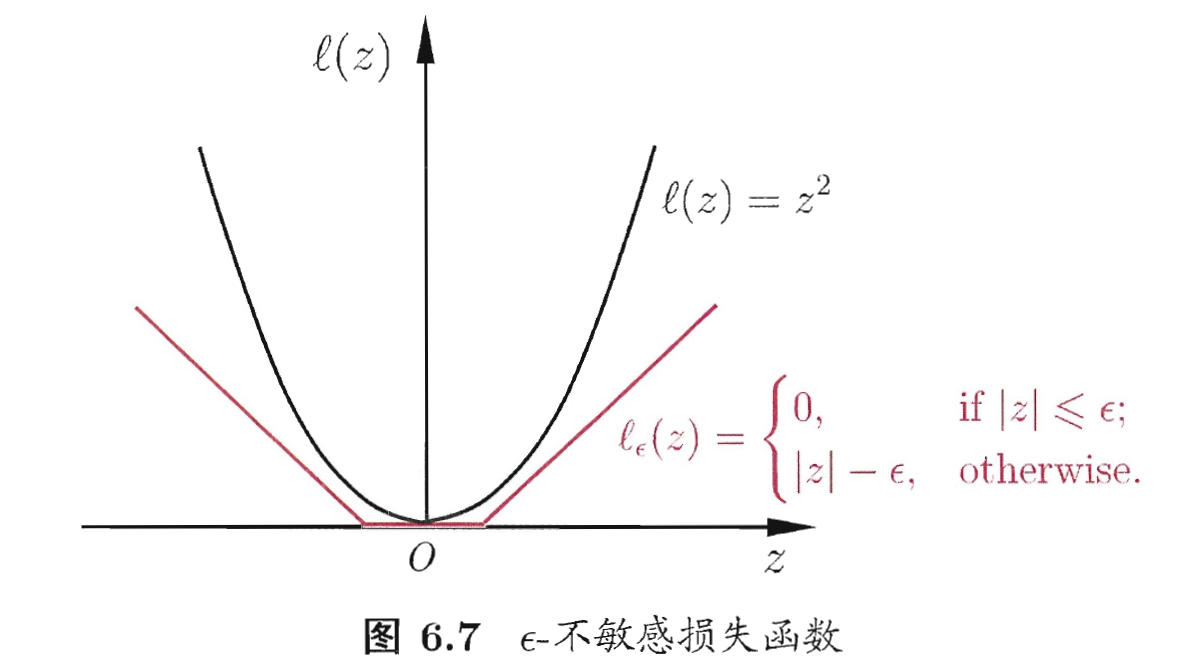
之间的差别绝对值大于 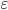 时才计算损失. 如下图, 这相当于以
时才计算损失. 如下图, 这相当于以 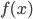 为中心, 构建了一个宽度为
为中心, 构建了一个宽度为 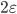 的间隔带, 若训练样本落入此间隔带, 则认为是被预测正确的.
的间隔带, 若训练样本落入此间隔带, 则认为是被预测正确的.
- 于是, SVR问题可形式化为:
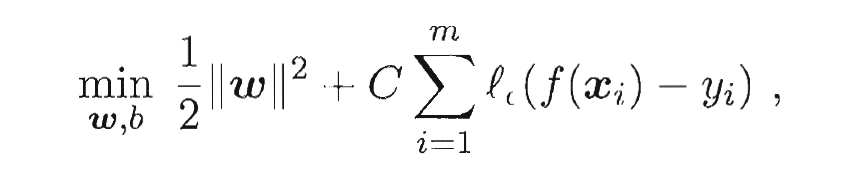
- 其中
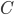 为正则化常数,
为正则化常数, 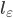 是
是 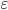 - 不敏感损失 (
- 不敏感损失 ( 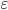 - insensitive loss )函数:
- insensitive loss )函数:
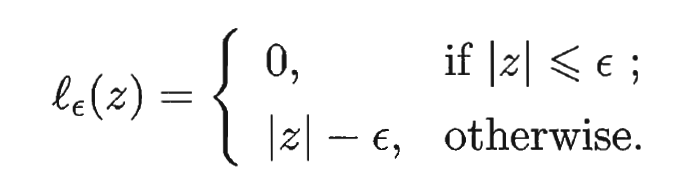
- 引入松弛变量
 和
和  , 可重写为:
, 可重写为:
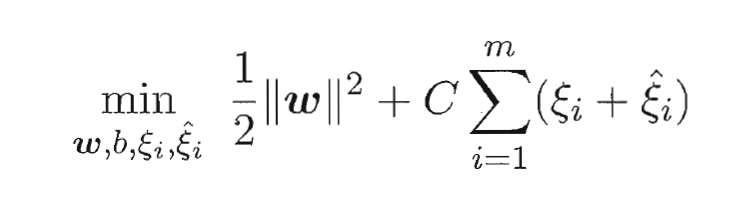
- 再令
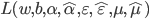 , 对
, 对 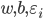 和
和 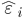 的偏导为零可得:
的偏导为零可得:
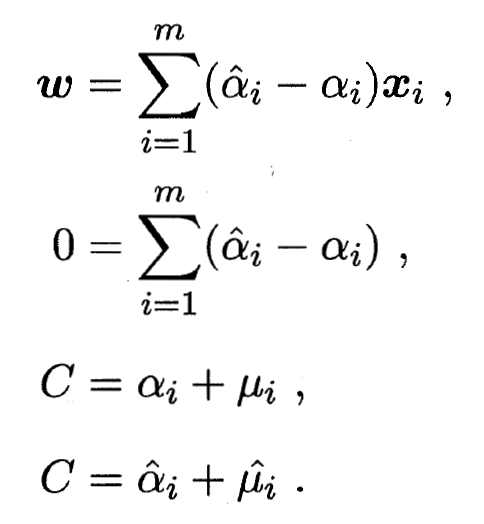
- 将式带入, 即可得到SVR的对偶问题:
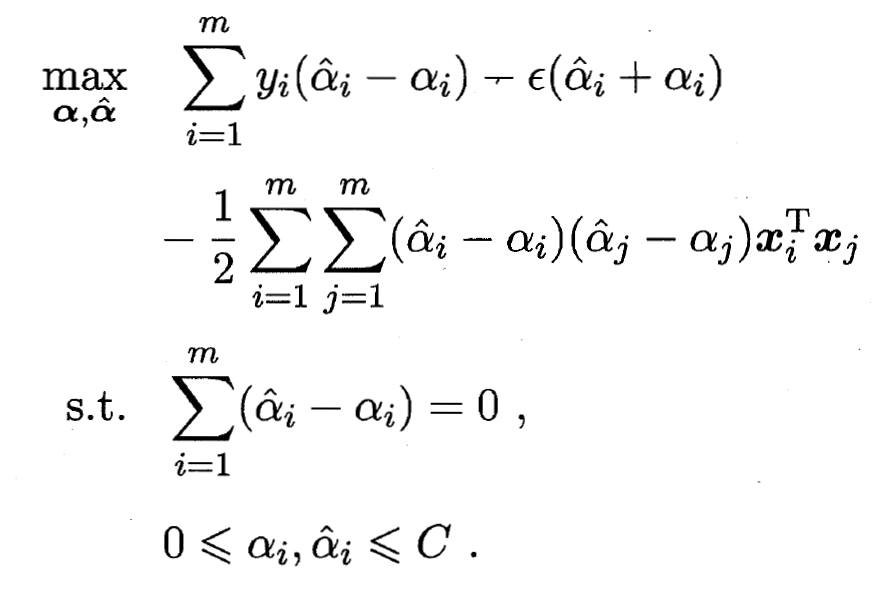
- 上述过程中满足KKT条件, 即要求:
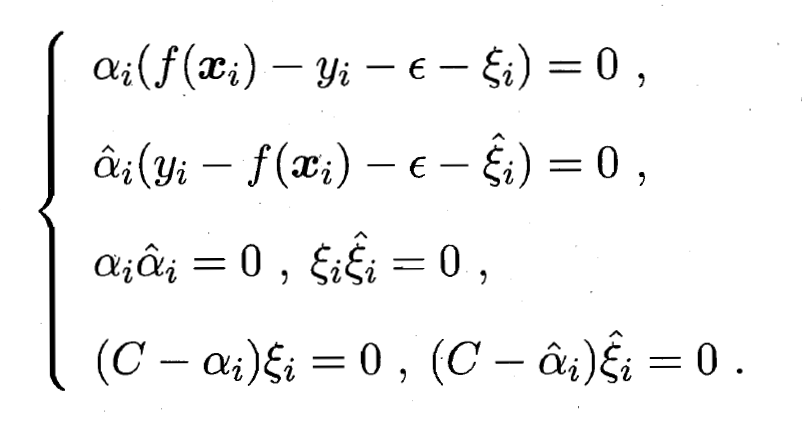
- 可以看出, 当且仅当
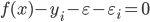 时
时 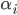 能取非零值, 当且仅当
能取非零值, 当且仅当 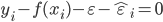 时
时 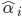 能取非零值. 换言之, 仅当样本
能取非零值. 换言之, 仅当样本 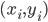 不落入
不落入 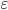 - 间隔带中, 相应的
- 间隔带中, 相应的 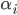 和
和 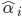 才能取非零值. 此外, 约束
才能取非零值. 此外, 约束 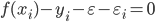 和
和 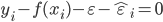 不能同时成立, 因此
不能同时成立, 因此 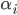 和
和 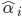 中至少有一个为零. 则SVR的解形如:
中至少有一个为零. 则SVR的解形如:
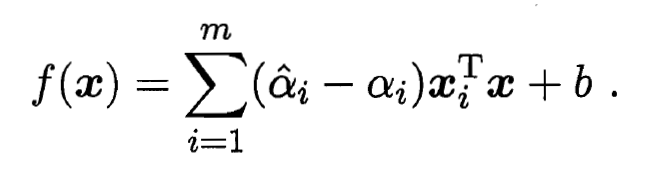
- 能使
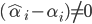 的样本即为SVR的支持向量, 他们必须落在
的样本即为SVR的支持向量, 他们必须落在 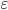 - 间隔带之外. 显然, SVR的支持向量仅是训练样本的一部分, 即其解仍具有稀疏性. 由KKT条件可看出, 对每个样本
- 间隔带之外. 显然, SVR的支持向量仅是训练样本的一部分, 即其解仍具有稀疏性. 由KKT条件可看出, 对每个样本 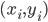 都有
都有 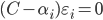 且
且 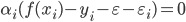 . 于是, 在得到
. 于是, 在得到 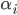 后, 若
后, 若 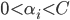 , 则必有
, 则必有 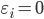 进而有:
进而有:
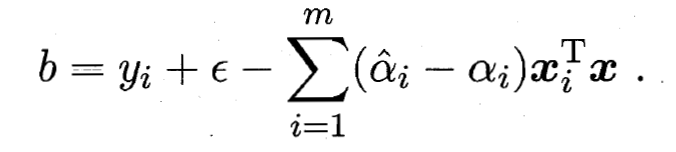
- 因此, 在求解得到
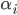 后, 理论上来说, 可任意选取满足
后, 理论上来说, 可任意选取满足 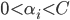 的样本求得
的样本求得  . 实践中长采用一种更鲁棒的办法: 选取多个(或所有)满足条件
. 实践中长采用一种更鲁棒的办法: 选取多个(或所有)满足条件 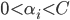 的样本求解
的样本求解  后取平均值. 若考虑特征映射形式, 相应的, 得到:
后取平均值. 若考虑特征映射形式, 相应的, 得到:
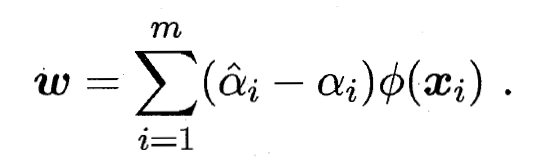
- 则SVR可表示为:
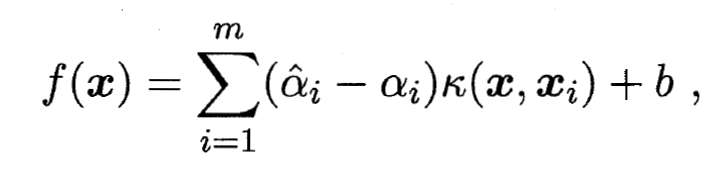
- 今天, 我们学习了SVM中的支持向量回归; 明天, 我们将继续学习SVM中的核方法.
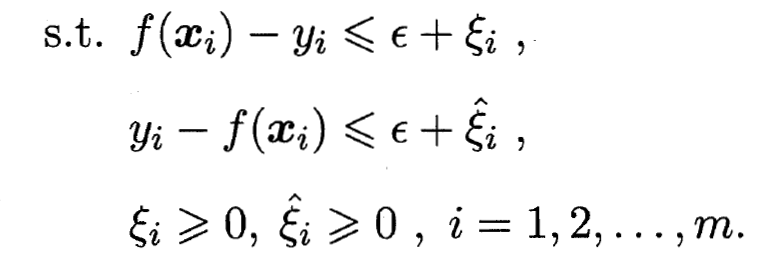
- 通过引入拉格朗日乘子 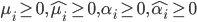 , 由拉格朗日乘子法可得到拉格朗日函数:
, 由拉格朗日乘子法可得到拉格朗日函数:
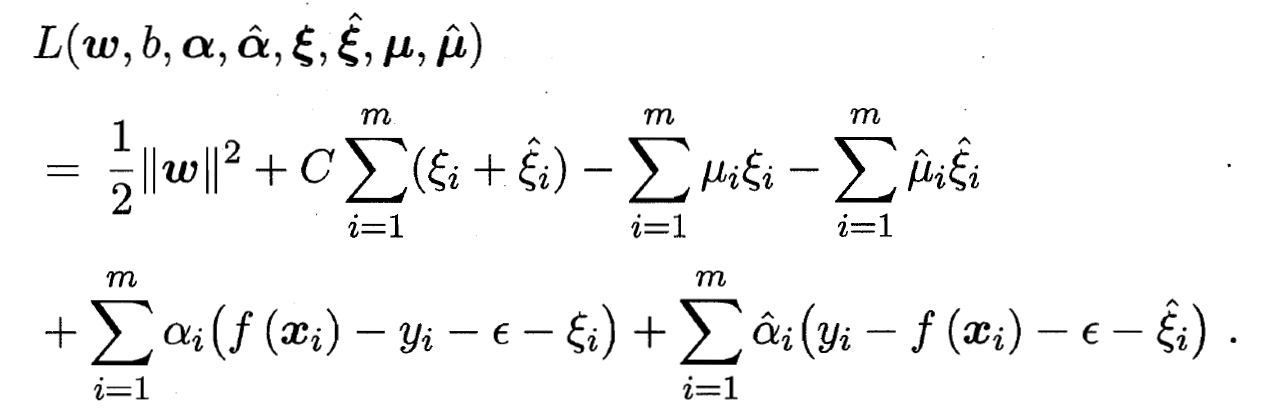
其中 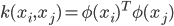 为核函数.
为核函数.
Be First to Comment