写在前面
- 在这个章节, 我们将从头推导一个神经网络的反向传播过程. 反向传播在神经网络中非常重要, 要理解透彻神经网络的学习过程, 需要好好消化一下这里的内容.
- 如果你对微积分还不够理解, 请先看微积分(一). 如果你对神经网络正向传播过程还不理解, 请先看神经网络(二)
误差
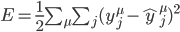
- 我们需要有一个指标来了解预测有多差, 也就是误差 (error).
- 这里
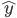 是预测值, y是真实值. 一个是所有输出单元j的和, 另一个是所有数据点
是预测值, y是真实值. 一个是所有输出单元j的和, 另一个是所有数据点 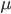 的和. 首先是内部这个对j的求和. 变量j代表网络输出单元. 所以这个内部的求和是指对于每一个输出单元, 计算预测值
的和. 首先是内部这个对j的求和. 变量j代表网络输出单元. 所以这个内部的求和是指对于每一个输出单元, 计算预测值 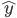 与真实值y之间的差的平方, 再求和. 另一个对
与真实值y之间的差的平方, 再求和. 另一个对 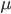 的求和是针对所有的数据点. 也就是说, 对每一个数据点, 计算其对应输出单元的方差和, 然后把每个数据点的方差和加在一起. 这就是你整个输出的总误差.
的求和是针对所有的数据点. 也就是说, 对每一个数据点, 计算其对应输出单元的方差和, 然后把每个数据点的方差和加在一起. 这就是你整个输出的总误差. - 选择SSE有几个原因: 误差的平方总是正的, 对大误差的惩罚大于小误差. 同时, 它对数学运算也更友好.
反向传播
- 依旧是上一个章节的例子, 再贴一下图:
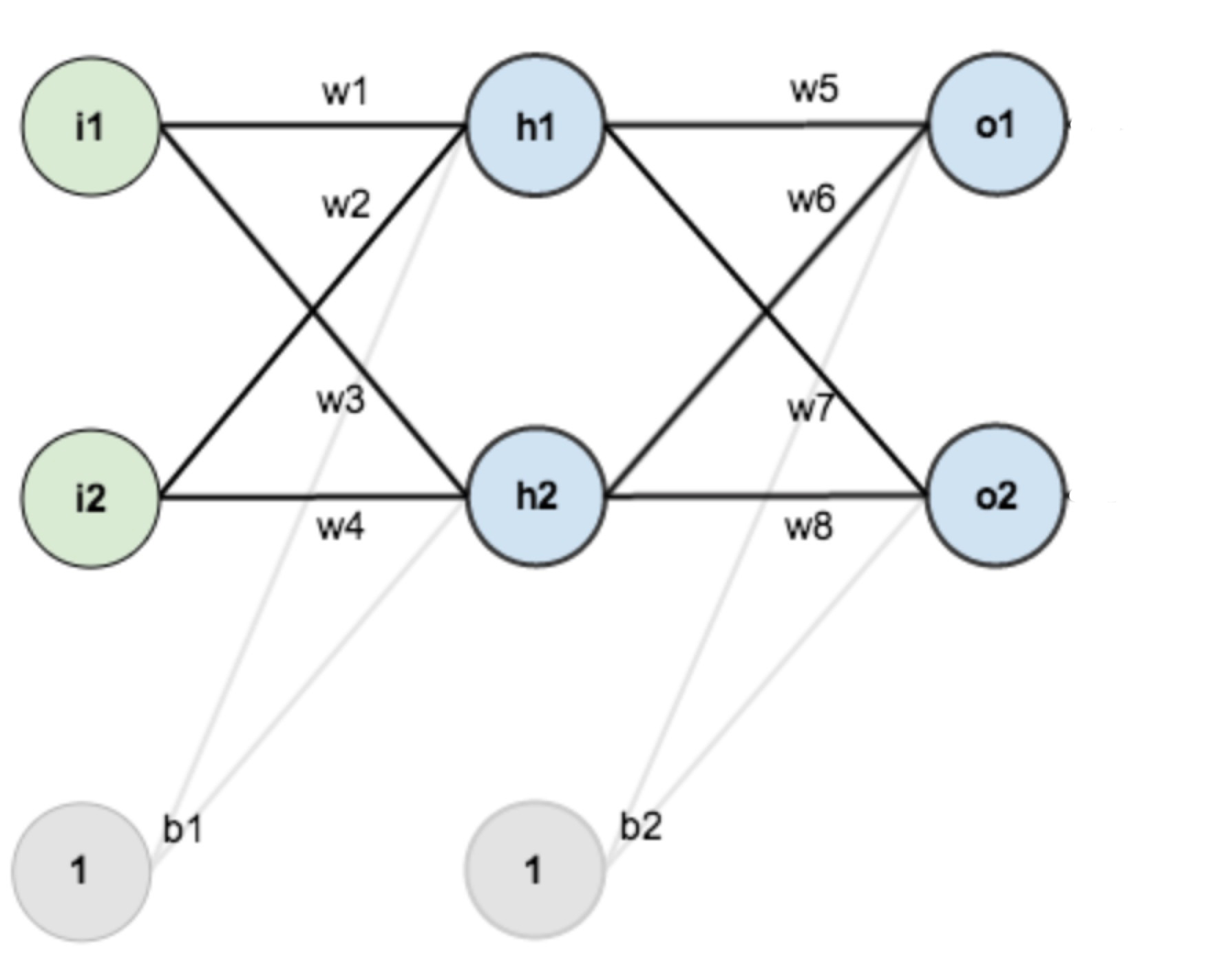
- 在上一个正向传播中, 我们是从Input->Hidden->Output, 而在反向传播中, 我们应该从总误差开始往上面推, 在这个图例, 就是从右边的Output Layer到左边的Input Layer, 一层一层的计算错误对节点的影响. 紧接着上一个章节, 我们假设正确的
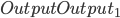 为
为 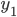 ,
, 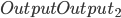 为
为 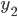 .
. - 总误差:
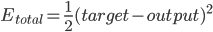
得出:
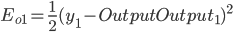
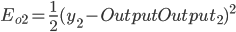
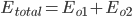
- Output Layer到Hidden Layer: 以
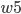 为例, 对
为例, 对 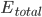 求偏导, 计算
求偏导, 计算 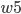 对
对 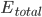 的影响.
的影响.
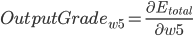
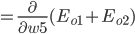
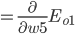
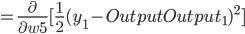
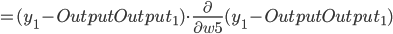
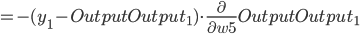
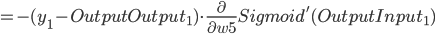
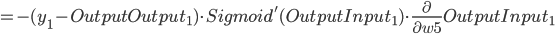
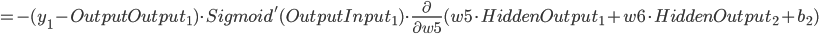
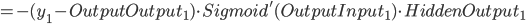
同理可得:
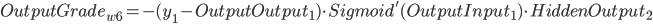
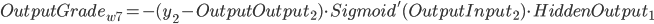
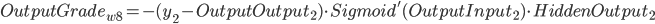
- ErrorTerm(
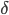 ),
), 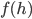 为激活函数,
为激活函数, 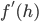 为激活函数的导数:
为激活函数的导数:
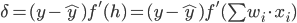
则有:
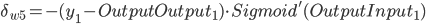
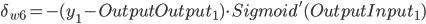
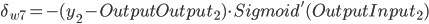
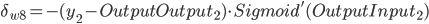
带入到OutputGrade:
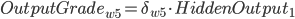
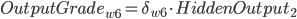
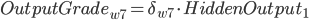
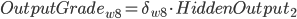
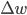 , 权重更新:
, 权重更新:
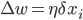
在这里
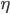 是学习率,
是学习率, 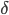 是ErrorTerm.
是ErrorTerm.则有:
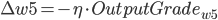
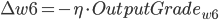
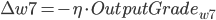
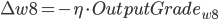
- 更新后的权重值:
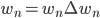
则有:
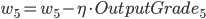
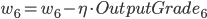
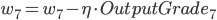
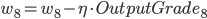
- Input Layer, 以
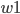 为例, 对
为例, 对 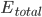 求偏导, 计算
求偏导, 计算 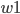 对
对 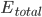 的影响(注意, 这里计算的时候Hidden Layer使用的是还未经过更新的权重值).
的影响(注意, 这里计算的时候Hidden Layer使用的是还未经过更新的权重值).
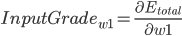
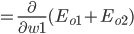
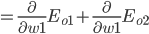
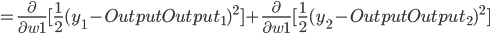
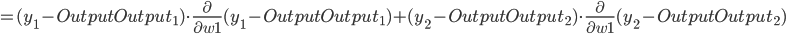
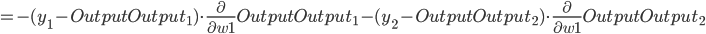
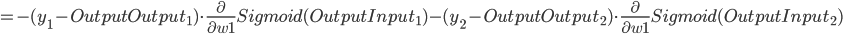







同理可推:



仔细看看:

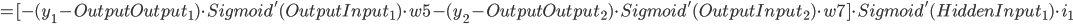

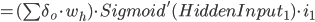
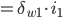
得出:
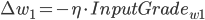
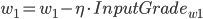
同理可得:
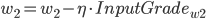
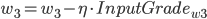
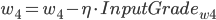
- 至此, 我们已经完整的将神经网络的学习过程(正反向传播)给推导了一遍.
写在后面
- 在这篇文章里面, 我们对反向传播进行了推导, 但这还仅仅是开始.
Be First to Comment