Press "Enter" to skip to content
写在前面
- 在上次的文章中, 大致的对微积分的思路与过程做了个介绍, 这次我们将进行更加深入的讨论.
关于d
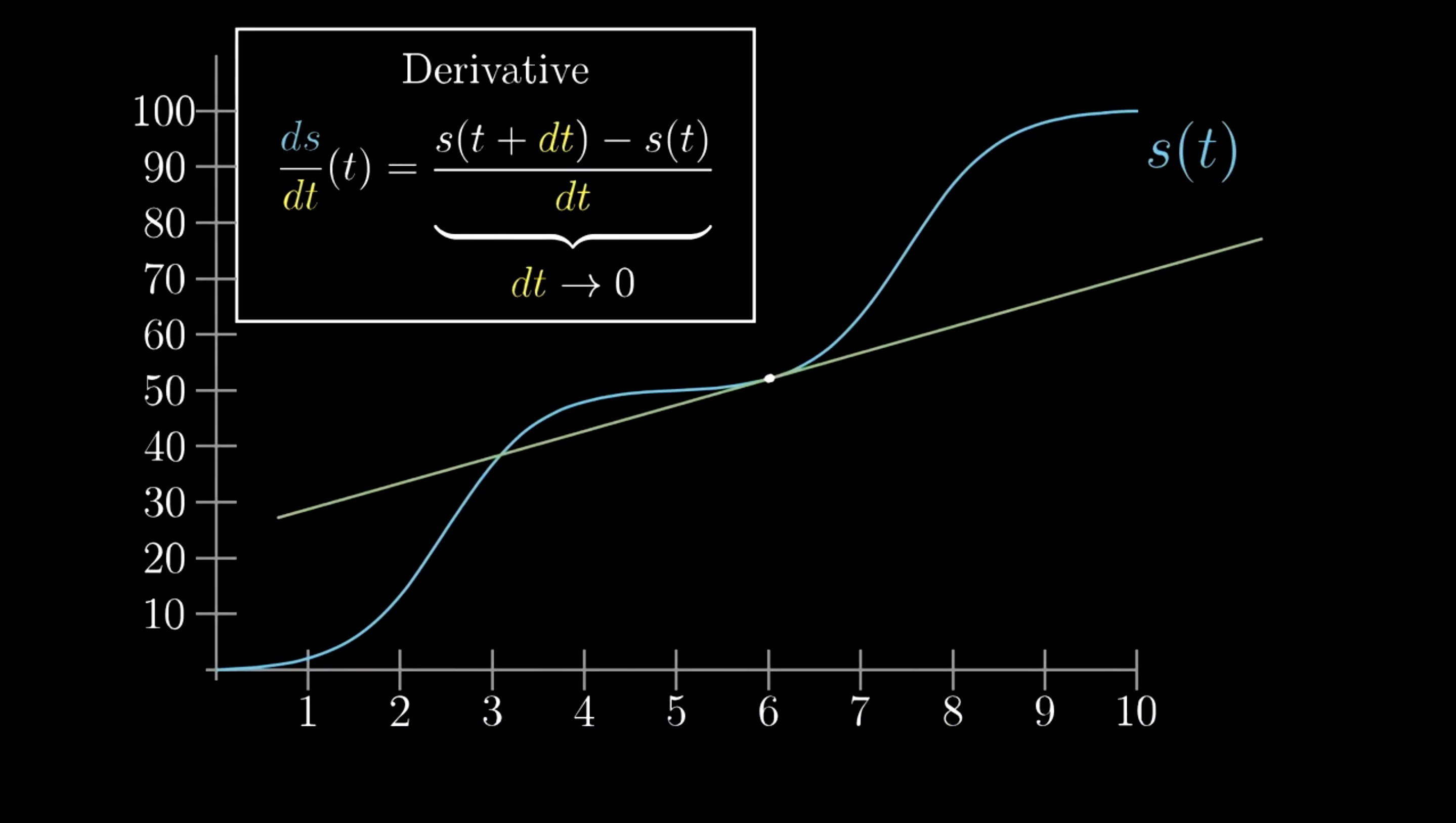
- 如图, 在汽车行驶速度的讨论中(
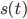 为汽车行驶时间与距离的关系函数 ), 我们将速度定义成
为汽车行驶时间与距离的关系函数 ), 我们将速度定义成 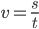 . 则小车在当前点的行驶速度为
. 则小车在当前点的行驶速度为 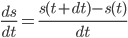 . 当dt的值非常小时, 我们近似的将其看做为这个点的切线. 而速度则是此切线的斜率.
. 当dt的值非常小时, 我们近似的将其看做为这个点的切线. 而速度则是此切线的斜率.
- 在微积分里, 我们都会采用这种思路来分析解决问题, 这里的dt是个非常微小的值, 却又是真实存在, 且不为零的.
- 在微积分里, 用d表示一个变量趋近于零.
一个简单的求导过程

- 如图, 我们假设现在要求小车在2秒的速度
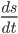 .
.
- 已知
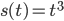 .
.
- 则
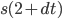 为第2秒到
为第2秒到 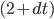 秒的距离差,
秒的距离差, 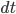 为时间上的变化, 极为微小.
为时间上的变化, 极为微小.
- 得出:
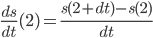
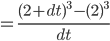
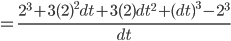
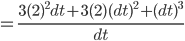
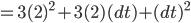
- 当dt逼近于零, 非常小的时候, 可以忽略后面的
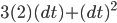 .
.
- 则可得出最后的结果
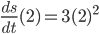 . 当然这个结果是有规律可循的, 这个我们接下来慢慢讲.
. 当然这个结果是有规律可循的, 这个我们接下来慢慢讲.
- 这个结果不仅仅对
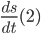 有效, 同样的, 对整个
有效, 同样的, 对整个 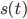 都有效.
都有效.
- 得出结果
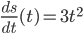 .
.
0秒时的速度

- 通过对上一题图中的观察, 我们详细观察在
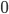 ~ (
~ ( 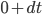 ) 秒间车轮的动态, 也就是
) 秒间车轮的动态, 也就是 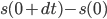 .
.
- 可以发现, 在
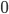 ~ (
~ ( 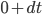 )之间, 车轮发生的位移非常小. 以至于
)之间, 车轮发生的位移非常小. 以至于 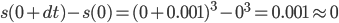 最终导致
最终导致 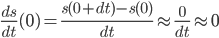 .
.
- 注意, 这里是近似为零, 由于这段时间行驶的距离非常小, 我们近似的将其作为零来处理.
写在最后
- 这个章节以小车的距离/时间曲线为例, 详细的讲解了对函数求解的思路与方法.
- 下一小节, 我们将会用图例的方式来对一些常用的求导公式进行讲解.
Related

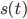 为汽车行驶时间与距离的关系函数 ), 我们将速度定义成
为汽车行驶时间与距离的关系函数 ), 我们将速度定义成 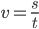 . 则小车在当前点的行驶速度为
. 则小车在当前点的行驶速度为 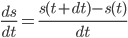 . 当dt的值非常小时, 我们近似的将其看做为这个点的切线. 而速度则是此切线的斜率.
. 当dt的值非常小时, 我们近似的将其看做为这个点的切线. 而速度则是此切线的斜率.
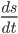 .
.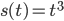 .
.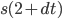 为第2秒到
为第2秒到 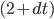 秒的距离差,
秒的距离差, 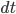 为时间上的变化, 极为微小.
为时间上的变化, 极为微小.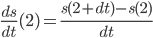
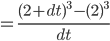
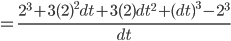
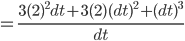
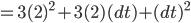
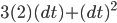 .
.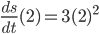 . 当然这个结果是有规律可循的, 这个我们接下来慢慢讲.
. 当然这个结果是有规律可循的, 这个我们接下来慢慢讲.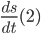 有效, 同样的, 对整个
有效, 同样的, 对整个 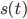 都有效.
都有效.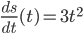 .
.
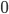 ~ (
~ ( 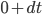 ) 秒间车轮的动态, 也就是
) 秒间车轮的动态, 也就是 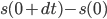 .
.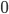 ~ (
~ ( 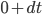 )之间, 车轮发生的位移非常小. 以至于
)之间, 车轮发生的位移非常小. 以至于 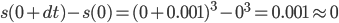 最终导致
最终导致 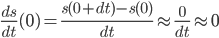 .
.
Be First to Comment