Example
得到癌症的概率是1%, 敏感性和特殊性都是90%, 癌症测试结果呈阳性的人患病的概率有多大?
得到癌症的概率:P(C) = 0.01
SENSITIVITY = 90%, 敏感性, 在P(C)中, 诊断的准确率为90%, 10%的人可能患有癌症, 却被诊断成正常人.
SPECITIVITY = 90%, 特异性, 在P(¬C)中, 诊断的正确率为90%, 10%的正常人被误诊为有癌症.
画图分析
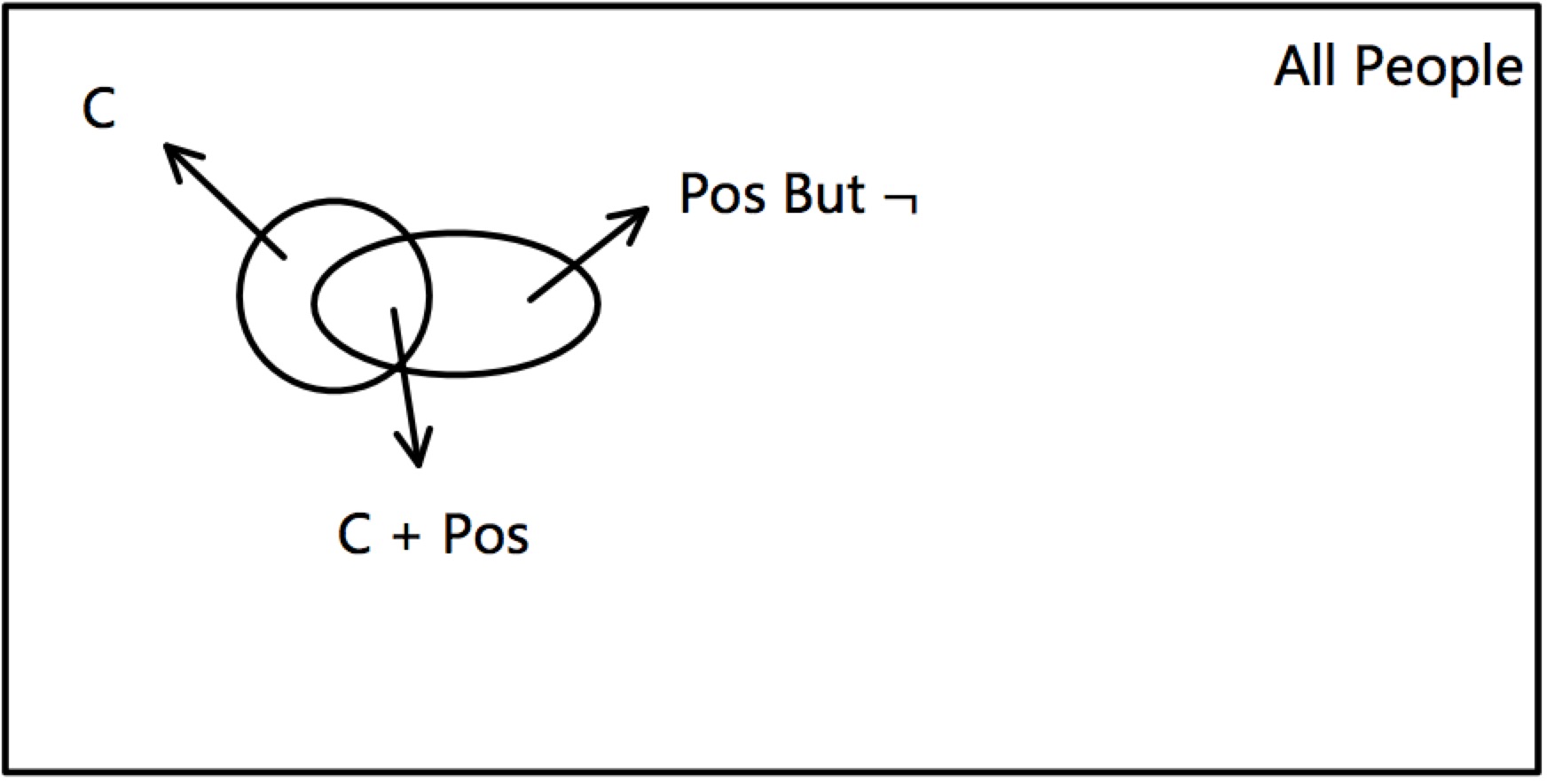
上图中, C表示患有癌症的人, C Pos表示患有癌症且被确诊的人, Pos Bu ¬表示被误诊为癌症的正常人.
问题: 癌症测试结果呈阳性的人患病的概率有多大?
假设这里一共有总共有1000个人(All_People)
Pos But ¬(正常人被误诊) = All_People * (1 - SPECITIVITY)
= 1000 * (1 - 0.9)
= 100
C(实际患有癌症的人) = All_People * P(C)
= 1000 * 0.01
= 10
C Pos(实际上患有癌症且被确诊的人) = C * SENSITIVITY
= 10 * 0.9
= 9
癌症测试结果呈阳性的所有人 = (C Pos(实际上患有癌症且被确诊的人)) + (Pos But ¬(正常人被误诊))
= 9 + 100
= 109
癌症测试结果呈阳性的人患病的概率 = (C Pos(实际上患有癌症且被确诊的人) ) / (癌症测试结果呈阳性的所有人)
= 9 / 109
= 0.083(四舍五入到小数点后三位)
先验与后验
Prior Probability(校验之前所得到的概率) * Test Evidence(测试本身获得的一些证据) = Posterior Probability(后验概率)
将测试中的某些证据加入先验概率中, 以获得联合概率.
Prior(先验)
癌症的先验概率: P(C) = 0.01 = 1%
非癌症的先验概率: P(¬C) = 1 − P(C)
= 0.99
SENSITIVITY(敏感性): P(Pos | C) = 0.9 = 90%
SPECITIVITY(特异性): P(Neg | ¬C) = 0.9 = 90%
被误诊为癌症概率: P(Pos | ¬C) = 1 − SPECITIVITY
= 0.1
Joint(联合概率)
癌症的联合概率: P(C, Pos) = P(C) * SENSITIVITY
= 0.01 * 0.9
= 0.009
非癌症的联合概率: P(¬C, Pos) = P(¬C) * P(Pos | ¬C)
= 0.99 * 0.1
= 0.099
Normalization(归一化)
数字归一, 比例保持不变, 确保他们相加之和为1.
后验概率求和 = 癌症的后验概率 + 非癌症的后验概率
检测为阳性的概率: P(Pos) = P(C, Pos) + P(¬C, Pos)
= 0.009 + 0.099
= 0.108
Posterior(后验概率)
癌症的后验概率: P(C | Pos) = 癌症的联合概率 / 检测为阳性的概率
= (P(C, Pos)) / (P(Pos))
= 0.009 / 0.108
= 0.0833
非癌症的后验概率: P(¬C | Pos) = 非癌症的联合概率 / 检测为阳性的概率
= (P(¬C, Pos)) / (P(Pos))
= 0.099 / 0.108
= 0.9167
后验概率求和: 癌症的后验概率 + 非癌症的后验概率 = P(C | Pos) + P(¬C | Pos)
= 0.0833 + 0.9167
= 1
Related

Be First to Comment