Press "Enter" to skip to content
写在前面
- 昨天, 我们对SVM进行了大致的介绍, 相信大家对支持向量机都有了个大致的了解, 今天我们将继续学习对偶问题.
对偶问题
- 我们希望求得大间隔划分超平面所对应的模型:
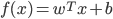
其中, 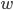 和
和  是模型参数. 注意到其本身是一个凸二次规划(Convex Quadratic Programming)问题, 能直接用现成的优化计算包求解, 但我们可以有更高效的办法. 使用拉格朗日乘子法可得到其'对偶问题'(Dual Problem). 具体来说, 就是对每条约束添加拉格朗日乘子
是模型参数. 注意到其本身是一个凸二次规划(Convex Quadratic Programming)问题, 能直接用现成的优化计算包求解, 但我们可以有更高效的办法. 使用拉格朗日乘子法可得到其'对偶问题'(Dual Problem). 具体来说, 就是对每条约束添加拉格朗日乘子 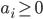 , 则该问题的拉格朗日函数可写为:
, 则该问题的拉格朗日函数可写为:
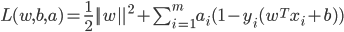
- 其中
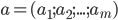 . 令
. 令 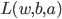 对
对 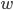 和
和  的偏导为零可得:
的偏导为零可得:
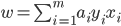
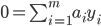
- 最终得到:
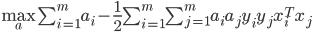
s.t. 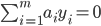
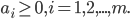
- 解出
 后, 求出
后, 求出 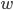 与
与  即可得到模型:
即可得到模型:
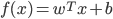
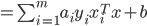
- 解出
 后, 求出
后, 求出 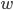 与
与  即可得到模型:
即可得到模型:
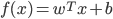
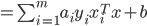
- 上述过程满足KKT(Karush-Kuhn-Tucker)条件, 即要求:
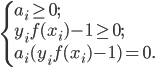
- 于是, 对任意训练样本
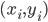 , 总有
, 总有 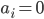 或
或 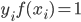 . 若
. 若 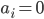 , 则该样本不会对
, 则该样本不会对 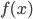 有任何影响; 若
有任何影响; 若 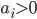 , 则必有
, 则必有 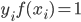 , 所对应的样本点位于最大间隔边界上, 是一个支持向量. 这显示出支持向量机的一个重要性质: 训练完成后, 大部分的训练样本都不需保留, 最终模型仅与支持向量有关.
, 所对应的样本点位于最大间隔边界上, 是一个支持向量. 这显示出支持向量机的一个重要性质: 训练完成后, 大部分的训练样本都不需保留, 最终模型仅与支持向量有关.
- 不难发现, 这是个二次规划问题, 可使用通用的二次规划算法来求解; 然而该问题的规模正比于训练样本数, 这回在实际任务中造成很大的开销. 为了避开这个障碍, 人们通过利用问题本身的特性, 提除了很多高效算法, SMO(Sequential Minimal Optimization)是其中一个著名的代表.
- SMO的基本思路是先固定
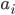 之外的所有参数, 然后求
之外的所有参数, 然后求 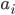 上的极值. 由于存在约束
上的极值. 由于存在约束 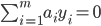 , 若固定
, 若固定 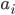 之外的其他变量, 则
之外的其他变量, 则 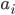 可由其他变量导出. 于是, SMO每次选择两个变量
可由其他变量导出. 于是, SMO每次选择两个变量 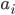 和
和 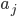 , 并固定其他参数. 这样, 在参数初始化后, SMO不断执行如下两个步骤直至收敛:
, 并固定其他参数. 这样, 在参数初始化后, SMO不断执行如下两个步骤直至收敛:
1.选取一对需更新的变量 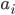 和
和 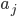 ;
;
2.固定 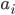 和
和 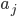 以外的参数, 求解获得更新后的
以外的参数, 求解获得更新后的 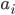 和
和 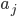 .
.
- SMO算法之所以高效, 恰由于在固定其他参数后, 仅优化两个参数的过程能做到非常高效. 具体来说, 仅考虑
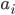 和
和 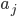 时, 可重写为:
时, 可重写为:
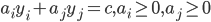
- 其中:
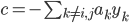
- 是使
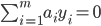 成立的常数. 用:
成立的常数. 用:
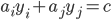
- 注意到对任意支持向量
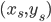 都有
都有 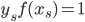 , 即:
, 即:
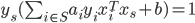
- 其中
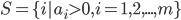 为所有支持向量的下标集. 理论上, 可选取任意支持向量并通过求解释获得
为所有支持向量的下标集. 理论上, 可选取任意支持向量并通过求解释获得  , 但现实任务中常采用一种更鲁棒的做法: 使用所有支持向量求解的平均值:
, 但现实任务中常采用一种更鲁棒的做法: 使用所有支持向量求解的平均值:
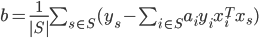
写在后面
- 今天, 我们学习了SVM的对偶问题, 并对其原理进行了大致的介绍.
- 明天, 我们将会继续学习, SVM的核函数.
Related
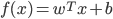
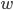 和
和  是模型参数. 注意到其本身是一个凸二次规划(Convex Quadratic Programming)问题, 能直接用现成的优化计算包求解, 但我们可以有更高效的办法. 使用拉格朗日乘子法可得到其'对偶问题'(Dual Problem). 具体来说, 就是对每条约束添加拉格朗日乘子
是模型参数. 注意到其本身是一个凸二次规划(Convex Quadratic Programming)问题, 能直接用现成的优化计算包求解, 但我们可以有更高效的办法. 使用拉格朗日乘子法可得到其'对偶问题'(Dual Problem). 具体来说, 就是对每条约束添加拉格朗日乘子 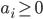 , 则该问题的拉格朗日函数可写为:
, 则该问题的拉格朗日函数可写为: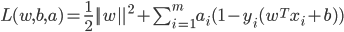
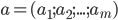 . 令
. 令 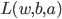 对
对 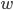 和
和  的偏导为零可得:
的偏导为零可得: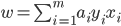
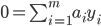
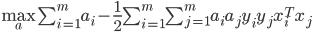
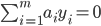
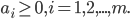
 后, 求出
后, 求出 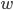 与
与  即可得到模型:
即可得到模型: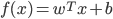
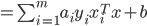
 后, 求出
后, 求出 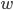 与
与  即可得到模型:
即可得到模型: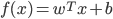
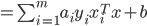
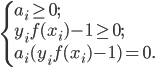
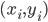 , 总有
, 总有 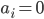 或
或 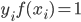 . 若
. 若 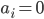 , 则该样本不会对
, 则该样本不会对 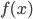 有任何影响; 若
有任何影响; 若 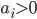 , 则必有
, 则必有 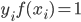 , 所对应的样本点位于最大间隔边界上, 是一个支持向量. 这显示出支持向量机的一个重要性质: 训练完成后, 大部分的训练样本都不需保留, 最终模型仅与支持向量有关.
, 所对应的样本点位于最大间隔边界上, 是一个支持向量. 这显示出支持向量机的一个重要性质: 训练完成后, 大部分的训练样本都不需保留, 最终模型仅与支持向量有关.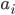 之外的所有参数, 然后求
之外的所有参数, 然后求 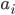 上的极值. 由于存在约束
上的极值. 由于存在约束 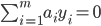 , 若固定
, 若固定 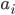 之外的其他变量, 则
之外的其他变量, 则 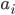 可由其他变量导出. 于是, SMO每次选择两个变量
可由其他变量导出. 于是, SMO每次选择两个变量 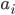 和
和 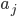 , 并固定其他参数. 这样, 在参数初始化后, SMO不断执行如下两个步骤直至收敛:
, 并固定其他参数. 这样, 在参数初始化后, SMO不断执行如下两个步骤直至收敛: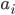 和
和 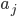 ;
;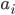 和
和 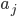 以外的参数, 求解获得更新后的
以外的参数, 求解获得更新后的 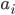 和
和 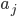 .
.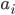 和
和 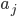 时, 可重写为:
时, 可重写为: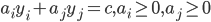
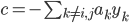
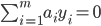 成立的常数. 用:
成立的常数. 用: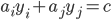
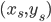 都有
都有 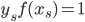 , 即:
, 即: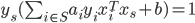
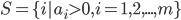 为所有支持向量的下标集. 理论上, 可选取任意支持向量并通过求解释获得
为所有支持向量的下标集. 理论上, 可选取任意支持向量并通过求解释获得  , 但现实任务中常采用一种更鲁棒的做法: 使用所有支持向量求解的平均值:
, 但现实任务中常采用一种更鲁棒的做法: 使用所有支持向量求解的平均值: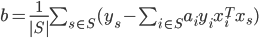
Be First to Comment