Press "Enter" to skip to content
写在前面
- 这篇文章中, 我们接着学习偏差与方差部分. 在学习的同时, 对于数学基础不是太好的童鞋, 最好能准备好google, 或者备一本<概率导论>.
偏差与方差
- '偏差-方差分解'(Bias-Variance Decomposition): 是解释学习算法泛化性能的一种重要工具. 偏差-方差分解试图对学习算法的期望泛化错误率进行拆解. 我们知道, 算法在不同训练集上学的的结果很可能不同, 即便这些训练集是来自同一个分布. 对测试样本
 , 令
, 令 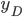 为
为  在数据集中的标记,
在数据集中的标记, 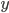 为
为  的真实标记,
的真实标记, 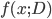 为训练集
为训练集  上学的模型
上学的模型 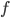 在
在  上的预测输出. 以回归任务为例, 学习算法的期望预测为:
上的预测输出. 以回归任务为例, 学习算法的期望预测为:
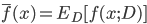
- 使用样本数相同的不同训练集产生的方差为:
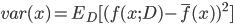
- 噪声为:
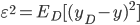
- 期望输出与真实标记的差别称为偏差(Bias):
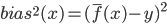
- 为了便于讨论, 假定噪声期望为0, 即
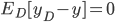 . 通过简单的多项式展开合并, 可对算法的期望泛化误差进行分解:
. 通过简单的多项式展开合并, 可对算法的期望泛化误差进行分解:
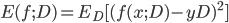
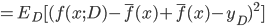
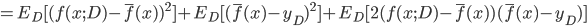
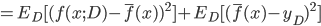
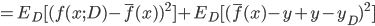
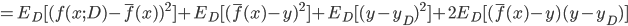
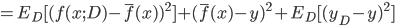
- 注意: 推导过程看不懂的, 可以拉到上面去对着看看, 一步一步往下推, 这里不难, 建议尝试一下. 这里的期望, 可以理解为均值.
- 最后得出, 泛化误差为偏差, 方差与噪声之和:
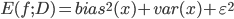
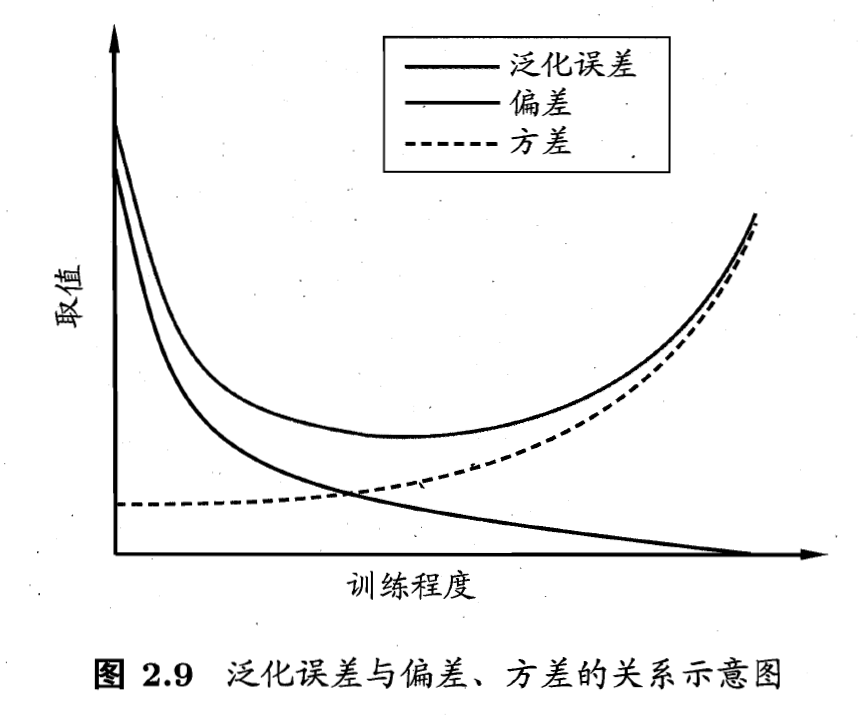
- 偏差-方差窘境(Bias-Variance Dilemma): 一般来说, 偏差与方差是有冲突的, 这称为偏差-方差窘境(Bias-Variance Dilemma). 如下图, 给定学习任务, 假定我们能控制学习算法的训练程度, 则在训练不足时, 学习器的拟合能力不够强, 训练数据的扰动不足以使学习器产生显著变化, 此时偏差主导了泛化错误率; 随着训练程度的加深, 学习器的拟合能力逐渐增强, 训练数据发生的扰动渐渐能被学习器学到, 方差逐渐主导了泛化错误率; 在训练程度充足后, 学习器的拟合能力已非常强, 训练数据发生的轻微扰动都会导致学习器发生显著变化, 若训练数据自身的, 非全局的特性被学习器学到了, 则将发生过拟合.
写在后面
- 这篇文章中内容虽然比较少, 可笔者还是建议大家都跟着推导一下, 这样有助于深刻理解里面的一些问题, 遇见不懂的概念, 可以及时google补充, 对后面的帮助会比较大.
- 明天, 我们将会继续学习下一个章节-线性模型.
Related
 , 令
, 令 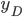 为
为  在数据集中的标记,
在数据集中的标记, 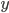 为
为  的真实标记,
的真实标记, 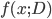 为训练集
为训练集  上学的模型
上学的模型 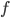 在
在  上的预测输出. 以回归任务为例, 学习算法的期望预测为:
上的预测输出. 以回归任务为例, 学习算法的期望预测为: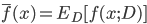
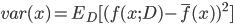
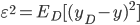
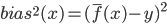
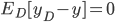 . 通过简单的多项式展开合并, 可对算法的期望泛化误差进行分解:
. 通过简单的多项式展开合并, 可对算法的期望泛化误差进行分解: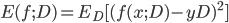
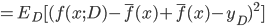
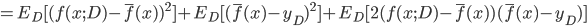
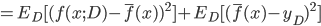
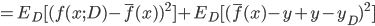
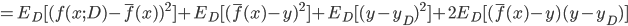
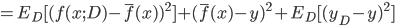
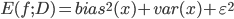

Be First to Comment