写在前面

• 昨天, 我们学习了集成学习中的结合策略; 今天, 我们将继续学习集成学习中的多样性.

误差-分歧分解

• 欲构建泛化能力强的集成, 个体学习器应'好而不同'. 现在我们来做一个简单的理论分析. 假定我们用个体学习器 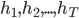通过加权平均法结合产生的集成来完成回归学习任务 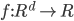. 对示例 , 定义学习器 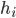的'分歧'(Ambiguity)为:

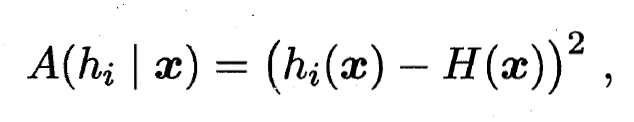
• 则集成的'分歧'是:

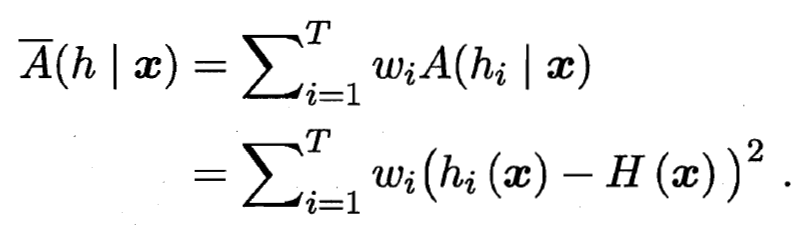
• 显然, 这里的'分歧'项表征了个体学习器在样本 上的不一致性, 即在一定程度上反映了个体学习器的多样性. 个体学习器 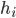和集成 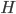的平方误差分别为:

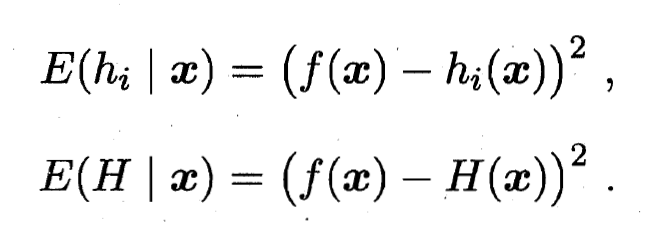
• 令 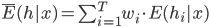表示个体学习器误差的加权均值, 有:

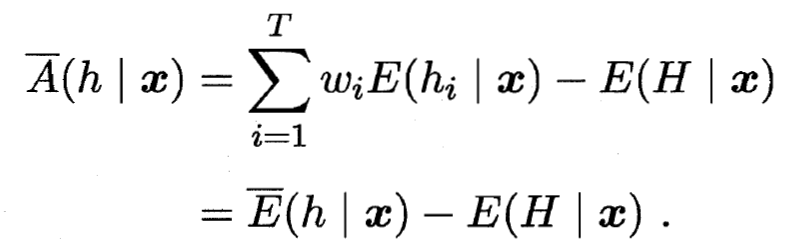
• 令 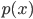表示样本的概率密度, 则在全样本上有:

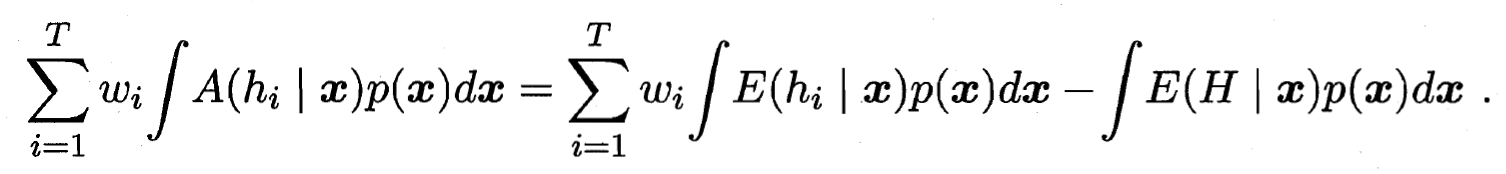
• 类似的, 个体学习器 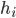在全样本上的泛化误差和分歧项分别为:

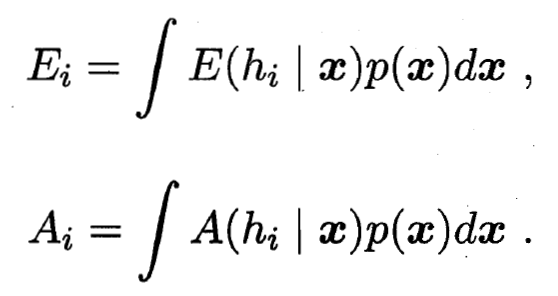
• 集成的泛化误差为:

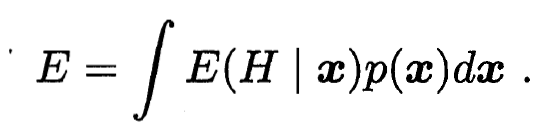
• 最后有:

写在后面

• 今天, 我们将继续学习了集成学习中的多样性; 明天, 我们将学习下一个章节, 聚类中的聚类任务.