Press "Enter" to skip to content
写在前面
- 昨天, 我们学习了SVM中的支持向量回归. 今天, 我们继续学习SVM中的核方法.
核方法
- 回顾前面两天的内容, 可以发现, 给定训练样本
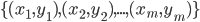 , 若不考虑偏移项
, 若不考虑偏移项  , 则无论SVM还是SVR, 学得的模型总能表示成核函数
, 则无论SVM还是SVR, 学得的模型总能表示成核函数 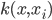 的线性组合. 不仅如此, 事实上我们有下面这个称为'表示定理'(Representer Theorem)的更一般的结论:
的线性组合. 不仅如此, 事实上我们有下面这个称为'表示定理'(Representer Theorem)的更一般的结论:
- [定理]: 令
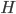 为核函数
为核函数 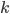 对应的再生核希尔伯特空间,
对应的再生核希尔伯特空间, 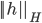 表示
表示 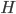 空间中关于
空间中关于  的函数, 对于任意单调递增函数
的函数, 对于任意单调递增函数 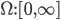 , 优化问题:
, 优化问题:
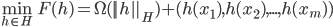
- 上式的解总可写为:
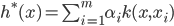
- 表示定理对损失函数没有限制, 对正则化项
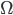 仅要求单调递增, 甚至不要求
仅要求单调递增, 甚至不要求 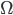 是凸函数, 意味着对于一般的损失函数和正则化项, 优化问题的最优解
是凸函数, 意味着对于一般的损失函数和正则化项, 优化问题的最优解 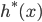 都可表示为核函数
都可表示为核函数 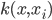 的线性组合; 这显示出核函数的巨大威力.
的线性组合; 这显示出核函数的巨大威力.
- 人们发展出一些列基于核函数的学习方法, 统称为'核方法'(Kernel Methods). 最常见的, 是通过'核化'(即引入核函数)来讲线性学习器拓展为非线性学习器, 从而得到'核线性判别分析'(Kernelized Linear Discriminant Analysis, 简称KLDA).
- 我们先假设可通过某种映射
 将样本映射到一个特征空间
将样本映射到一个特征空间 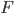 , 然后在
, 然后在 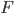 中执行线性判别分析, 以求得:
中执行线性判别分析, 以求得:
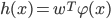
- 则KLDA的学习目标是:
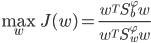
- 其中
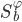 和
和 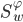 分别为训练样本在特征空间
分别为训练样本在特征空间 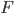 中的类间散度矩阵和类内散度矩阵. 令
中的类间散度矩阵和类内散度矩阵. 令 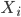 表示第
表示第 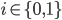 类样本的集合, 其样本数为
类样本的集合, 其样本数为 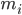 ; 总样本数
; 总样本数 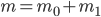 . 第
. 第 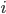 类样本在特征空间
类样本在特征空间 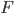 中的均值为:
中的均值为:
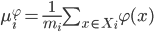
- 两个三度矩阵分别为:
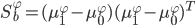
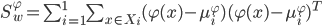
- 通常我们难以知道映射
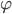 的具体形式, 因此使用核函数
的具体形式, 因此使用核函数 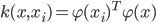 来隐式地表达这个映射和特征空间
来隐式地表达这个映射和特征空间 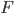 . 把
. 把 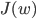 作为损失函数
作为损失函数 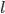 , 再令
, 再令 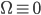 , 由表示定理, 函数
, 由表示定理, 函数 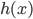 可写为:
可写为:
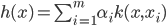
- 于是有:
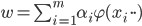
- 令
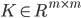 为核函数
为核函数 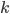 所对应的核矩阵,
所对应的核矩阵, 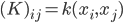 . 令
. 令 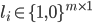 为第
为第 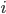 类样本的指示向量, 即
类样本的指示向量, 即 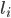 的第
的第 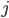 个分量为0. 再令:
个分量为0. 再令:
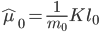
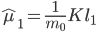
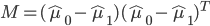
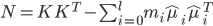
- 于是等价为:
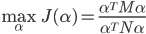
- 显然, 使用线性判别分析求解方法可得到
 , 进而可得到投影函数
, 进而可得到投影函数 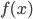 .
.
写在后面
- 今天, 我们学习了SVM中的核方法. 明天, 我们将学习下一章, 贝叶斯分类器中的贝叶斯决策论.
Related
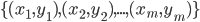 , 若不考虑偏移项
, 若不考虑偏移项  , 则无论SVM还是SVR, 学得的模型总能表示成核函数
, 则无论SVM还是SVR, 学得的模型总能表示成核函数 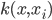 的线性组合. 不仅如此, 事实上我们有下面这个称为'表示定理'(Representer Theorem)的更一般的结论:
的线性组合. 不仅如此, 事实上我们有下面这个称为'表示定理'(Representer Theorem)的更一般的结论: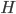 为核函数
为核函数 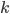 对应的再生核希尔伯特空间,
对应的再生核希尔伯特空间, 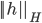 表示
表示 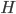 空间中关于
空间中关于  的函数, 对于任意单调递增函数
的函数, 对于任意单调递增函数 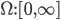 , 优化问题:
, 优化问题: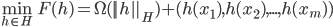
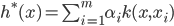
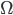 仅要求单调递增, 甚至不要求
仅要求单调递增, 甚至不要求 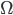 是凸函数, 意味着对于一般的损失函数和正则化项, 优化问题的最优解
是凸函数, 意味着对于一般的损失函数和正则化项, 优化问题的最优解 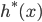 都可表示为核函数
都可表示为核函数 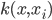 的线性组合; 这显示出核函数的巨大威力.
的线性组合; 这显示出核函数的巨大威力. 将样本映射到一个特征空间
将样本映射到一个特征空间 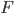 , 然后在
, 然后在 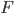 中执行线性判别分析, 以求得:
中执行线性判别分析, 以求得: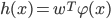
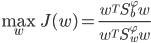
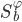 和
和 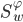 分别为训练样本在特征空间
分别为训练样本在特征空间 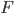 中的类间散度矩阵和类内散度矩阵. 令
中的类间散度矩阵和类内散度矩阵. 令 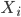 表示第
表示第 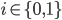 类样本的集合, 其样本数为
类样本的集合, 其样本数为 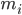 ; 总样本数
; 总样本数 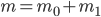 . 第
. 第 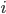 类样本在特征空间
类样本在特征空间 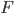 中的均值为:
中的均值为: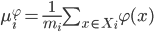
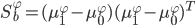
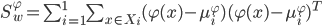
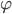 的具体形式, 因此使用核函数
的具体形式, 因此使用核函数 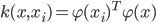 来隐式地表达这个映射和特征空间
来隐式地表达这个映射和特征空间 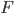 . 把
. 把 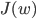 作为损失函数
作为损失函数 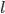 , 再令
, 再令 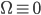 , 由表示定理, 函数
, 由表示定理, 函数 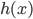 可写为:
可写为: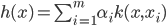
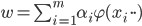
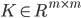 为核函数
为核函数 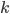 所对应的核矩阵,
所对应的核矩阵, 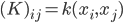 . 令
. 令 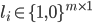 为第
为第 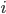 类样本的指示向量, 即
类样本的指示向量, 即 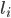 的第
的第 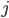 个分量为0. 再令:
个分量为0. 再令: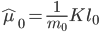
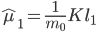
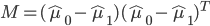
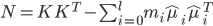
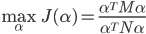
 , 进而可得到投影函数
, 进而可得到投影函数 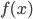 .
.
Be First to Comment