Press "Enter" to skip to content
写在前面
- 昨天, 我们学习了SVM中的对偶问题. 今天, 我们继续学习SVM中的核函数部分知识.
核函数
- 在讨论开始前, 我们假设训练样本是线性可分的, 即存在一个划分超平面能将训练样本正确分类. 然而在现实任务中, 原始样本空间内也许并不存在一个能正确划分两类样本的超平面. 对这样的问题, 可将样本从原始空间映射到一个更高纬的特征空间, 使得样本在这个特征空间内线性可分.
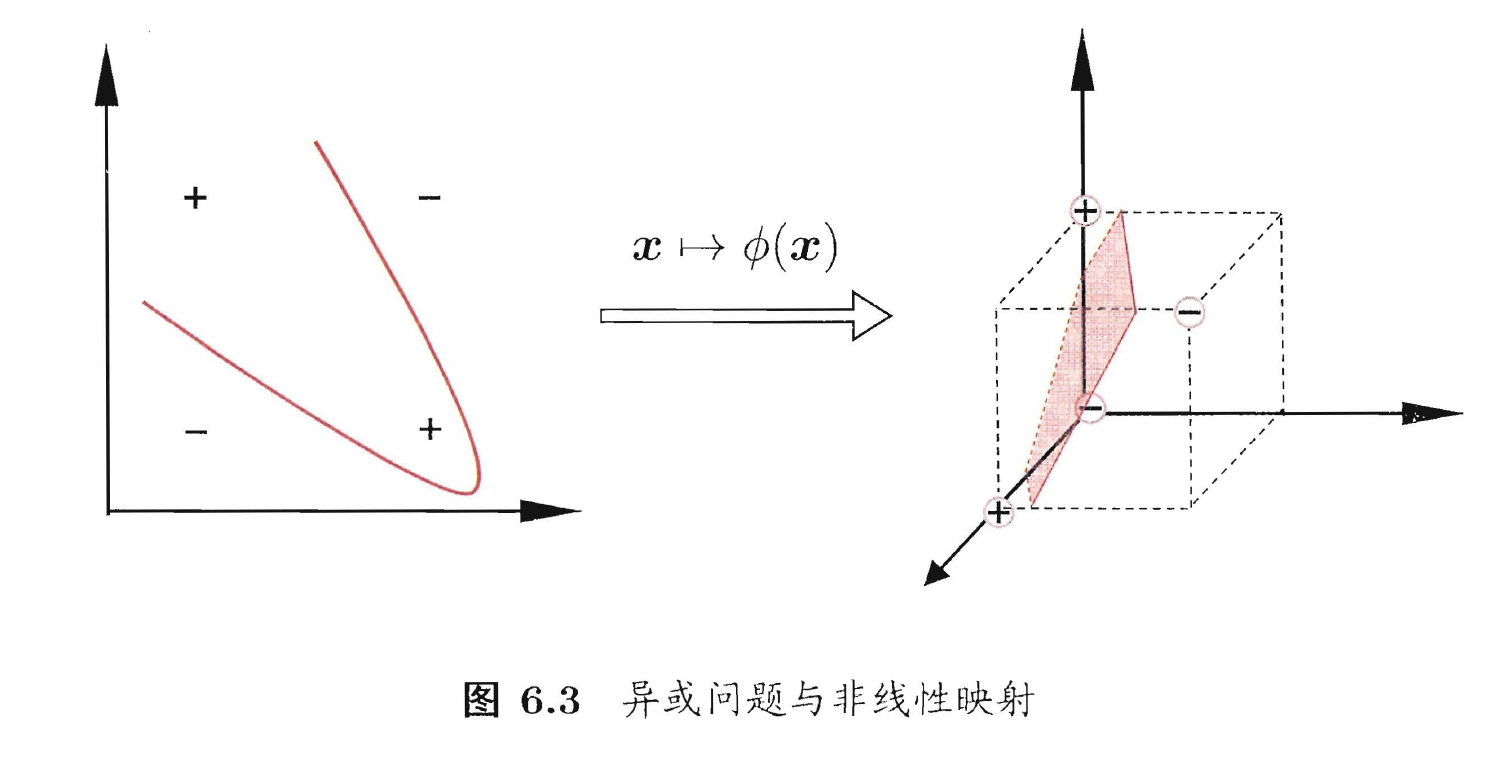
- 如上图, 若将原始的二维空间映射到一个合适的三维空间, 就能找到一个合适的划分超平面. 幸运的是, 如果原始空间是有限维, 即属性数有限, 那么一定存在一个高维特征空间使样本可分. 令
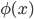 表示将
表示将  映射后的特征向量, 于是, 在特征空间中划分超平面所对应的模型可表示为:
映射后的特征向量, 于是, 在特征空间中划分超平面所对应的模型可表示为:
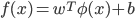
- 其中
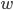 和
和  是模型参数, 则有:
是模型参数, 则有:
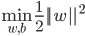
s.t. 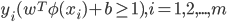
- 其对偶问题是:
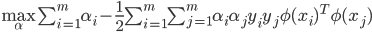
s.t. 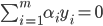
- 设想:
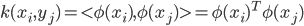
- 于是:
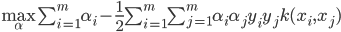
s.t. 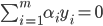
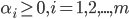
- 求解后可得到:
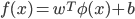
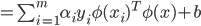
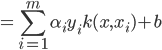
- 这里的函数
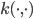 就是'核函数'(Kernel Function). 模型最优解可通过训练样本的核函数展开, 这一展式亦称'支持向量展式'(Support Vector Expansion).
就是'核函数'(Kernel Function). 模型最优解可通过训练样本的核函数展开, 这一展式亦称'支持向量展式'(Support Vector Expansion).
- 显然, 若一直合适映射
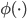 的具体形式, 则可写出核函数
的具体形式, 则可写出核函数 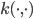 . 但在显示任务中, 我们通常不知道
. 但在显示任务中, 我们通常不知道 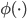 是什么形式, 那么, 合适的核函数是否一定存在呢? 什么样的函数能做核函数呢? 我们有如下的定理:
是什么形式, 那么, 合适的核函数是否一定存在呢? 什么样的函数能做核函数呢? 我们有如下的定理:

- 上述定理表明, 主要一个对称函数所对应的核矩阵半定义, 它就能作为核函数使用. 事实上, 对于一个半正定核矩阵, 总能找到一个与之对应的映射
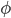 . 换言之, 任何一个核函数都隐式地定义了一个称为'再生核希尔伯特空间'(Reproducing Kernel Hilbert Space, 简称RKHS)的特征空间.
. 换言之, 任何一个核函数都隐式地定义了一个称为'再生核希尔伯特空间'(Reproducing Kernel Hilbert Space, 简称RKHS)的特征空间.
- 通过前面的讨论可知, 我们希望样本在特征空间内线性可分, 因此特征空间的好坏对支持向量机的性能至关重要. 需注意的是, 在不知道特征映射的形式时, 我们并不知道什么样的核函数是合适的, 而核函数也仅是隐式的定义了这个特征空间. 于是, '核函数选择'成为支持向量机的最大变数. 若核函数选择不合适, 则意味着将样本映射到了一个不合适的特征空间, 很可能导致性能不佳, 下图列出了几种常用的核函数:

- 此外, 还可通过函数组合得到, 例如:
1.若 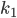 和
和 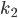 为核函数, 则对于任意正数
为核函数, 则对于任意正数 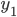 ,
, 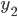 , 其线性组合:
, 其线性组合: 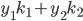 也是核函数;
也是核函数;
2.若 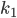 和
和 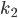 为核函数, 则核函数的直积:
为核函数, 则核函数的直积: 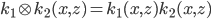 也是核函数;
也是核函数;
3.若 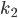 为核函数, 则对于任意函数
为核函数, 则对于任意函数 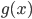 :
: 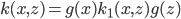 也是核函数.
也是核函数.
写在后面
- 今天, 我们介绍了SVM中核函数的部分知识. 明天, 我们将继续学习SVM中的软间隔与正则化部分.
Related

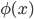 表示将
表示将  映射后的特征向量, 于是, 在特征空间中划分超平面所对应的模型可表示为:
映射后的特征向量, 于是, 在特征空间中划分超平面所对应的模型可表示为: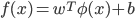
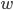 和
和  是模型参数, 则有:
是模型参数, 则有: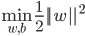
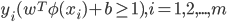
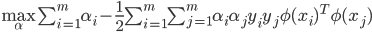
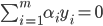
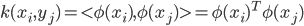
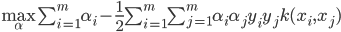
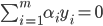
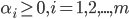
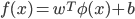
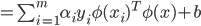
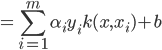
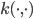 就是'核函数'(Kernel Function). 模型最优解可通过训练样本的核函数展开, 这一展式亦称'支持向量展式'(Support Vector Expansion).
就是'核函数'(Kernel Function). 模型最优解可通过训练样本的核函数展开, 这一展式亦称'支持向量展式'(Support Vector Expansion).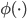 的具体形式, 则可写出核函数
的具体形式, 则可写出核函数 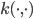 . 但在显示任务中, 我们通常不知道
. 但在显示任务中, 我们通常不知道 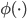 是什么形式, 那么, 合适的核函数是否一定存在呢? 什么样的函数能做核函数呢? 我们有如下的定理:
是什么形式, 那么, 合适的核函数是否一定存在呢? 什么样的函数能做核函数呢? 我们有如下的定理:
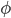 . 换言之, 任何一个核函数都隐式地定义了一个称为'再生核希尔伯特空间'(Reproducing Kernel Hilbert Space, 简称RKHS)的特征空间.
. 换言之, 任何一个核函数都隐式地定义了一个称为'再生核希尔伯特空间'(Reproducing Kernel Hilbert Space, 简称RKHS)的特征空间.
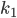 和
和 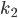 为核函数, 则对于任意正数
为核函数, 则对于任意正数 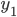 ,
, 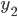 , 其线性组合:
, 其线性组合: 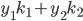 也是核函数;
也是核函数;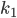 和
和 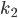 为核函数, 则核函数的直积:
为核函数, 则核函数的直积: 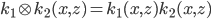 也是核函数;
也是核函数;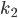 为核函数, 则对于任意函数
为核函数, 则对于任意函数 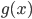 :
: 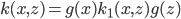 也是核函数.
也是核函数.
Be First to Comment