Press "Enter" to skip to content
写在前面
- 在大致了解神经网络了之后, 我们今天来学习下支持向量机相关的知识.
间隔与支持向量
- 给定训练样本集
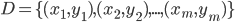 ,
, 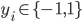 , 分类学习最基本的想法就是基于训练集
, 分类学习最基本的想法就是基于训练集  在样本空间中找到一个划分超平面, 将不同类别的样本分开. 但能将训练样本分开的划分超平面可能有很多, 如下图:
在样本空间中找到一个划分超平面, 将不同类别的样本分开. 但能将训练样本分开的划分超平面可能有很多, 如下图:
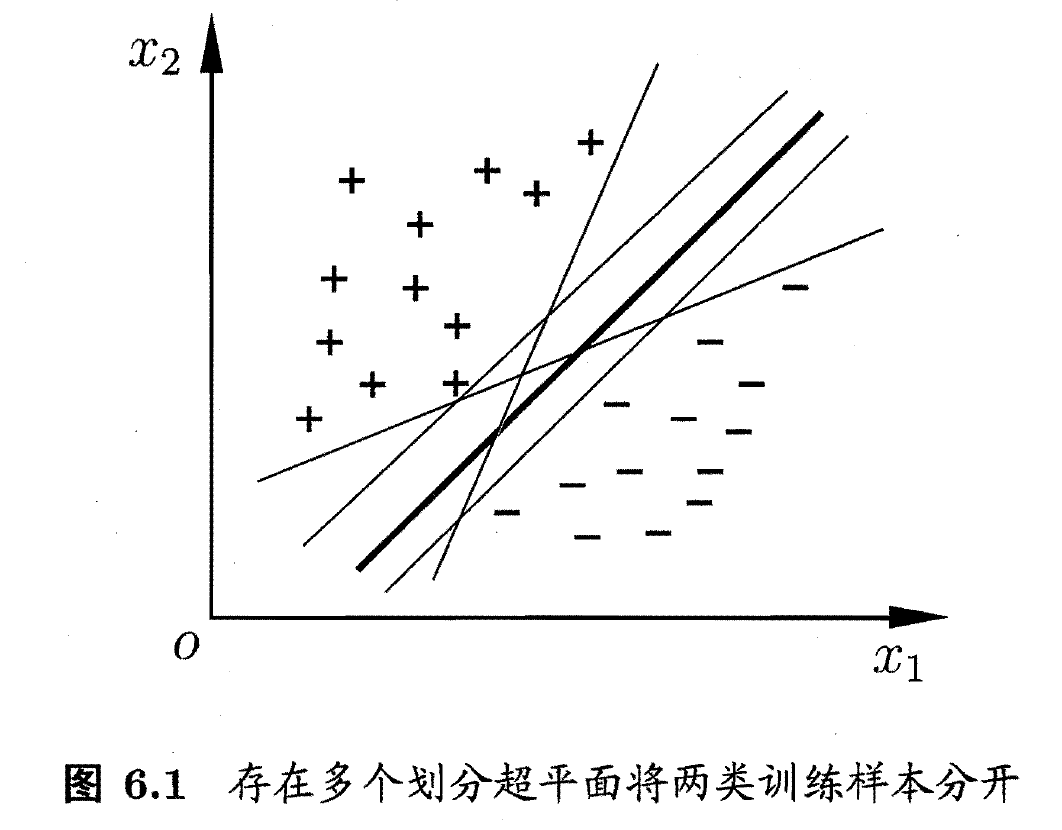
- 直观上看, 应该去找位于两类训练样本'正中间'的划分超平面, 因为该划分超平面对训练样本局部扰动的'容忍'性最好. 例如, 由于训练集的局限性或噪声的因素, 训练集外的样本可能比上图中的训练样本更接近两个类的分隔界, 这将是许多划分超平面出现错误, 二红色的超平面受影响最小. 换言之, 这个划分超平面所产生的分类结果是最鲁棒的, 对未见实例的泛化能力最强. 在样本空间中, 划分超平面可通过如下线性方程来描述:

其中  为法向量, 决定了超平面的方向;
为法向量, 决定了超平面的方向;  为位移项, 决定了超平面与原点之间的距离. 显然, 划分超平面可被法向量
为位移项, 决定了超平面与原点之间的距离. 显然, 划分超平面可被法向量 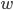 和位移
和位移  确定, 下面我们将其记为
确定, 下面我们将其记为  . 样本空间中任意点
. 样本空间中任意点  到超平面
到超平面  的距离可写为:
的距离可写为:

- 假设超平面
 能将训练样本正确分类, 即对于
能将训练样本正确分类, 即对于  , 若
, 若  , 则有
, 则有  ; 若
; 若  , 则有
, 则有  . 令:
. 令:

- 可以发现, 距离超平面最近的这几个训练样本点使上式的等号成立, 他们被称为'支持向量'(Support Vector), 两个异类支持向量到超平面的距离之和为:

它被称为'间隔'(Margin)

- 欲找到具有'最大间隔'(Maximum Margin)的划分超平面, 也就是要找到能满足上式约束的参数
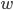 和
和  , 使得
, 使得  最大, 即:
最大, 即:

s.t. 
- 显然, 为了最大化间隔, 仅需最大化
 , 这等价于最小化
, 这等价于最小化  . 于是, 上式可以重写为:
. 于是, 上式可以重写为:

s.t. 
这就是支持向量机(Support Vector Machine, 简称SVM)的基本型.
写在最后
- 在本文中, 我们学习了SVM的一些基本概念.
- 明天, 我们将会学习对偶问题.
Related
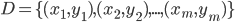 ,
, 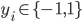 , 分类学习最基本的想法就是基于训练集
, 分类学习最基本的想法就是基于训练集  在样本空间中找到一个划分超平面, 将不同类别的样本分开. 但能将训练样本分开的划分超平面可能有很多, 如下图:
在样本空间中找到一个划分超平面, 将不同类别的样本分开. 但能将训练样本分开的划分超平面可能有很多, 如下图:

 为法向量, 决定了超平面的方向;
为法向量, 决定了超平面的方向;  为位移项, 决定了超平面与原点之间的距离. 显然, 划分超平面可被法向量
为位移项, 决定了超平面与原点之间的距离. 显然, 划分超平面可被法向量 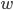 和位移
和位移  确定, 下面我们将其记为
确定, 下面我们将其记为  . 样本空间中任意点
. 样本空间中任意点  到超平面
到超平面  的距离可写为:
的距离可写为:
 能将训练样本正确分类, 即对于
能将训练样本正确分类, 即对于  , 若
, 若  , 则有
, 则有  ; 若
; 若  , 则有
, 则有  . 令:
. 令:


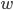 和
和  , 使得
, 使得  最大, 即:
最大, 即:

 , 这等价于最小化
, 这等价于最小化  . 于是, 上式可以重写为:
. 于是, 上式可以重写为:

Be First to Comment