写在前面
- 今天, 我们继续学习神经网络中的全局最小与局部极小.
全局最小与局部极小
- 若用
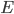 表示神经网络在训练集上的误差, 则它显然是关于连接权
表示神经网络在训练集上的误差, 则它显然是关于连接权 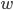 和阈值
和阈值 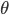 的函数. 此时, 神经网络的训练过程可看做一个参数寻优过程, 即在参数空间中, 寻找一组最优参数使得
的函数. 此时, 神经网络的训练过程可看做一个参数寻优过程, 即在参数空间中, 寻找一组最优参数使得 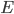 最小.
最小. - 我们常会谈到两种'最优': '局部极小'(Local Minimum)和'全局最小'(Global Minimum). 对
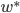 和
和 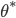 , 若存在
, 若存在 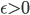 使得:
使得:
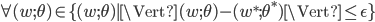
都有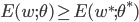 成立, 则
成立, 则 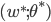 为局部极小解; 若对参数空间中的任意
为局部极小解; 若对参数空间中的任意 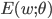 都有
都有 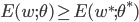 , 则
, 则 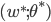 为局部最小解. 直观地看, 局部极小解是参数空间中的某个点, 其邻域点的误差函数值均不下雨该店的函数值; 全局最小解则是值参数空间中所有点的误差函数值均不小于该点的误差函数值. 两者对应的
为局部最小解. 直观地看, 局部极小解是参数空间中的某个点, 其邻域点的误差函数值均不下雨该店的函数值; 全局最小解则是值参数空间中所有点的误差函数值均不小于该点的误差函数值. 两者对应的 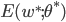 分别称为误差函数的局部极小值和全局最小值.
分别称为误差函数的局部极小值和全局最小值. - 显然, 参数空间内梯度为零的点, 只要其误差函数值小于邻点的误差函数值, 也就是局部极小点; 可能存在多个局部极小值, 但却只会有一个全局最小值. 也就是说, '全局最小'一定是'局部最小', 反之则不成立.
- 基于梯度的搜索是使用最为广泛的参数寻优方法. 在此类方法中, 我们从某些初始解出发, 迭代寻找最优参数值. 每次迭代中, 我们先计算误差函数在当前点的梯度, 然后根据梯度确定搜索方向.
- 在现实任务中, 人们常采用以下策略来试图'跳出'局部极小, 从而进一步接近全局最小:
1.以多组不同参数值初始化多个神经网络, 按标准方法训练后, 取其中误差最小的解作为最终参数. 这相当于从多个不同的初始点开始搜索, 这样就可能陷入不同的局部极小, 从中进行选择有可能获得更接近全局最小的结果.
2.使用'模拟退火'(Simulated Annealing)技术, 模拟退火在每一步都以一定的概率接受比当前解更差的结果, 从而有助于'跳出'局部极小. 在每步迭代过程中, 接受'次优解'的概率要随着时间的推移而逐渐降低, 从而保证算法稳定.
3.使用随机梯度下降. 与标准梯度下降法精确计算梯度不同, 随机梯度下降法在计算梯度时加入了随机因素, 于是, 即便陷入局部极小点, 它计算出的梯度仍可能不为零, 这样就有机会跳出局部极小继续搜索.
4.遗传算法(Genetic Algorithms)
写在后面
- 今天, 我们学习了神经网络中的全局最小与局部极小, 这一部分仅仅是对一些寻找全局最小的方法和算法进行了介绍, 如果对其中某些算法深感兴趣的童鞋, 可以详细了解下.
- 明天, 我们将继续学习其他神经网络.
Be First to Comment