Press "Enter" to skip to content
写在前面
- 今天, 我们继续学习决策树的最后一个小节, 多变量决策树. 本文中的内容会比较少, 也为大家留下了查漏补缺的时间, 如若前面有些问题还未弄清楚, 可以适当的补充数学知识, 倒回去看前面的内容. 学而时习之, 可以为师矣.
多变量决策树
- 若我们把每个属性视为坐标空间中的一个坐标轴, 则
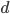 个属性描述的样本就对应了
个属性描述的样本就对应了 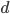 维空间中的一个数据点, 对样本分类则意味着在这个坐标空间中寻找不同类样本的分类便捷. 决策树所形成的分类边界有一个明显的特点: 轴平行(axis-parallel), 即它的分类边界由若干个与坐标轴平行的分段组成. 这样的分类边界使得学习结果有较好的可解释性, 因为每一段划分都直接对应了某个属性取值. 但在学习任务的真实分类边界比较复杂时, 必须使用很多段划分才能获得较好的近似. 此时的决策树会相当复杂, 由于要进行大量的属性测试, 预测时间开销会很大.
维空间中的一个数据点, 对样本分类则意味着在这个坐标空间中寻找不同类样本的分类便捷. 决策树所形成的分类边界有一个明显的特点: 轴平行(axis-parallel), 即它的分类边界由若干个与坐标轴平行的分段组成. 这样的分类边界使得学习结果有较好的可解释性, 因为每一段划分都直接对应了某个属性取值. 但在学习任务的真实分类边界比较复杂时, 必须使用很多段划分才能获得较好的近似. 此时的决策树会相当复杂, 由于要进行大量的属性测试, 预测时间开销会很大.
- 若能使用斜的划分边界, 则决策树模型将大为简化. '多变量决策树'(multivariate decision tree)就是能实现这样的'斜划分'甚至更复杂划分的决策树. 以实现斜划分的多变量决策树为例, 在此类决策树中, 非叶节点不再是仅对某个属性, 二十对属性的线性组合进行测试; 换言之, 每个非叶结点是一个形如
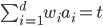 的线性分类器, 其中
的线性分类器, 其中 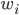 是属性
是属性 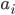 的权重,
的权重, 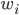 和
和 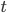 可在该节点所含的样本集和属性集上学的. 于是, 传统的'单变量决策树'(univariate decision tree)不同, 在多变量决策树的学习过程中, 不是为每个非叶借点寻找一个最优划分属性, 二十视图建立一个合适的线性分类器.
可在该节点所含的样本集和属性集上学的. 于是, 传统的'单变量决策树'(univariate decision tree)不同, 在多变量决策树的学习过程中, 不是为每个非叶借点寻找一个最优划分属性, 二十视图建立一个合适的线性分类器.
写在后面
- 到这里, 我们关于决策树的学习已经告一段落.
- 明天, 我们会继续下一个章节-神经网络中的神经元模型, 感知机与多层网络两个小节进行学习. 在开始学习前, 我希望大家能够利用今天余下的时间, 补充微积分知识, 附上本人写的微积分系列链接: 微积分(一).
Related
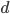 个属性描述的样本就对应了
个属性描述的样本就对应了 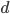 维空间中的一个数据点, 对样本分类则意味着在这个坐标空间中寻找不同类样本的分类便捷. 决策树所形成的分类边界有一个明显的特点: 轴平行(axis-parallel), 即它的分类边界由若干个与坐标轴平行的分段组成. 这样的分类边界使得学习结果有较好的可解释性, 因为每一段划分都直接对应了某个属性取值. 但在学习任务的真实分类边界比较复杂时, 必须使用很多段划分才能获得较好的近似. 此时的决策树会相当复杂, 由于要进行大量的属性测试, 预测时间开销会很大.
维空间中的一个数据点, 对样本分类则意味着在这个坐标空间中寻找不同类样本的分类便捷. 决策树所形成的分类边界有一个明显的特点: 轴平行(axis-parallel), 即它的分类边界由若干个与坐标轴平行的分段组成. 这样的分类边界使得学习结果有较好的可解释性, 因为每一段划分都直接对应了某个属性取值. 但在学习任务的真实分类边界比较复杂时, 必须使用很多段划分才能获得较好的近似. 此时的决策树会相当复杂, 由于要进行大量的属性测试, 预测时间开销会很大.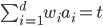 的线性分类器, 其中
的线性分类器, 其中 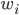 是属性
是属性 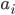 的权重,
的权重, 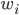 和
和 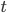 可在该节点所含的样本集和属性集上学的. 于是, 传统的'单变量决策树'(univariate decision tree)不同, 在多变量决策树的学习过程中, 不是为每个非叶借点寻找一个最优划分属性, 二十视图建立一个合适的线性分类器.
可在该节点所含的样本集和属性集上学的. 于是, 传统的'单变量决策树'(univariate decision tree)不同, 在多变量决策树的学习过程中, 不是为每个非叶借点寻找一个最优划分属性, 二十视图建立一个合适的线性分类器.
Be First to Comment