Press "Enter" to skip to content
写在前面
- 在这篇文章中, 我们将会介绍决策树中的剪枝处理, 连续值与缺失值处理.
剪枝处理
- 剪枝(Pruning)是决策树学习算法对付'过拟合'的主要手段. 决策树剪枝的基本策略有'预剪枝'(Prepruning)和'后剪枝'(Postpruning). 预剪枝是指在决策树生成过程中, 对每个节点在划分前先进行估计, 若当前节点的划分不能带来决策树泛化性能提升, 则停止划分并将当前结点标记为叶结点; 后剪枝则是先从训练集生成一颗完整的决策树, 然后自底向上地对非叶结点进行考察, 若将该结点对应的子树替换为叶结点能带来决策树泛化性能提升, 则将该子树替换为叶结点. 在这里, 我们可以使用留出法, 即预留一部分数据用作'验证集'以进行性能评估.
预剪枝
- 预剪枝基于信息增益准则, 预剪枝使得决策树的很多分值都没有'展开', 这不仅降低了过拟合的风险, 还显著减少了决策树的训练时间开销和测试时间开销. 另一方面, 有些分值的当前划分虽不能提升泛化性能, 甚至可能导致泛化性能暂时下降, 但在其基础上进行的后续划分却有可能导致性能显著提高; 预剪枝基于'贪心'本质禁止这些分支展开, 给预剪枝决策树带来了欠拟合的风险.
后剪枝
- 后剪枝先从训练集生成一颗完整的决策树. 后剪枝决策树通常比预剪枝决策树保留了更多的分支. 一般情形下, 后剪枝决策树的欠拟合风险很小, 泛化性能往往优于预剪枝决策树. 但后剪枝过程是在生成完全决策树之后进行的, 并且要自底向上地对树中所有非叶结点进行逐一考察, 因此其训练时间开销比未剪枝决策树和预剪枝决策树都要大得多.
连续与缺失值
- 连续值处理, 由于连续属性的可取值数目不在有限, 因此, 不能直接根据连续属性的可取值来对节点进行划分. 此时, 连续属性离散化技术可派上用场. 最简单的策略是采用二分法(bi-partition)对连续属性进行处理, 这正是
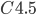 决策树算法中采用的机制.
决策树算法中采用的机制.
- 给定样本集
 和连续属性
和连续属性  , 假定
, 假定  在
在  上出现了
上出现了 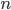 个不同的取值, 将这些值从小到大进行排序, 记为
个不同的取值, 将这些值从小到大进行排序, 记为 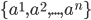 . 基于划分点
. 基于划分点 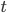 可将
可将  分为子集
分为子集 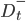 和
和 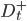 , 其中
, 其中 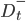 包含那些在属性
包含那些在属性  上取值不大于
上取值不大于 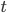 的样本, 而
的样本, 而 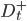 则包含那些在属性
则包含那些在属性  上取值大于
上取值大于 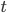 的样本. 显然, 对相邻的属性取值
的样本. 显然, 对相邻的属性取值 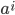 与
与 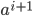 来说,
来说, 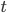 在区间
在区间 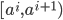 中任意取值所产生的划分结果相同. 因此, 对连续属性
中任意取值所产生的划分结果相同. 因此, 对连续属性  , 我们可考察包含
, 我们可考察包含 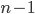 个元素的候选划分点集合:
个元素的候选划分点集合:
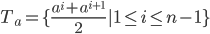
- 即把区间
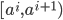 的中位点
的中位点 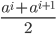 作为候选划分点. 然后我们就可以像离散属性值一样来考察这些划分点, 选取最优的划分点进行样本集合的划分. 对信息增益公式稍加改造则有:
作为候选划分点. 然后我们就可以像离散属性值一样来考察这些划分点, 选取最优的划分点进行样本集合的划分. 对信息增益公式稍加改造则有: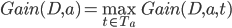
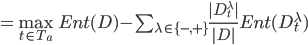 其中,
其中, 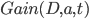 是样本集
是样本集  基于划分点
基于划分点 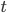 二分后的信息增益. 于是我们就可选择使
二分后的信息增益. 于是我们就可选择使 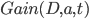 最大化的划分点.
最大化的划分点.
- 需注意的是, 与离散属性不同, 若当前结点划分属性为连续属性, 该属性还可作为其后代结点的划分属性.
缺失值处理
- 现实任务中常会遇到不完整样本, 即样本的某些属性值缺失. 尤其是在属性数目较多的情况下, 往往会有大量样本出现缺失值. 如果简单地放弃不完整样本, 仅使用无缺失值的样本来进行学习, 显然是对数据信息极大的浪费.
- 我们需要解决两个问题:
- 如何在属性值缺失的情况下进行划分属性选择?
- 给定划分属性, 若样本在该属性上的值缺失, 如何对样本进行划分?
- 给定训练集
 和属性
和属性  , 令
, 令 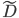 表示
表示  中在属性
中在属性  上没有缺失值的样本子集. 对问题1, 显然我们仅可根据
上没有缺失值的样本子集. 对问题1, 显然我们仅可根据 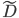 来判断属性
来判断属性  的优劣. 假定属性
的优劣. 假定属性  有
有 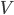 个可取值
个可取值 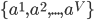 , 令
, 令 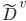 表示
表示 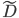 中在属性
中在属性  上取值为
上取值为 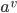 的样本子集,
的样本子集, 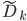 表示
表示 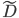 中属于第
中属于第 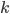 类
类 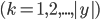 的样本子集, 则显然有
的样本子集, 则显然有 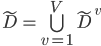 . 假定我们为每个样本
. 假定我们为每个样本  赋予一个权重
赋予一个权重 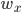 , 并定义:
, 并定义: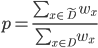
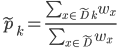
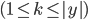
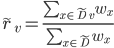
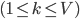
- 直观的看, 对属性
 ,
, 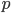 表示无缺失值样本所占的比例,
表示无缺失值样本所占的比例, 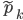 表示无缺失值样本中
表示无缺失值样本中 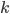 类所占的比例,
类所占的比例, 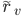 则表示无缺失值样本中在属性
则表示无缺失值样本中在属性  上取值
上取值 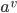 的样本所占的比例. 显然,
的样本所占的比例. 显然, 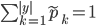 ,
, 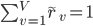 , 基于上述定义, 我们可将信息增益计算式推广为:
, 基于上述定义, 我们可将信息增益计算式推广为: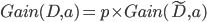
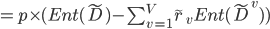
- 则有:
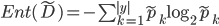
- 对问题2, 若样本
 在划分属性
在划分属性  上的取值已知, 则将
上的取值已知, 则将  划入与其取值对应的子结点, 且样本权值在子结点中保持为
划入与其取值对应的子结点, 且样本权值在子结点中保持为 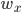 . 若样本
. 若样本  在划分属性
在划分属性  上的取值未知, 则将
上的取值未知, 则将  同时划入所有子结点, 且样本权值在于属性值
同时划入所有子结点, 且样本权值在于属性值 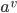 对应的子结点中调整为
对应的子结点中调整为 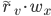 ; 直观的看, 这就是让同一个样本以不同的概率划入到不同的子结点中去.
; 直观的看, 这就是让同一个样本以不同的概率划入到不同的子结点中去.
- C4.5算法使用了上述解决方案.
写在后面
- 在这篇文章中, 介绍了决策树中如何对剪枝处理, 并且介绍了C4.5算法中连续值与缺失值处理的方法.
- 明天, 我们将会继续学习多变量决策树.
Related
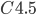 决策树算法中采用的机制.
决策树算法中采用的机制. 和连续属性
和连续属性  , 假定
, 假定  在
在  上出现了
上出现了 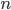 个不同的取值, 将这些值从小到大进行排序, 记为
个不同的取值, 将这些值从小到大进行排序, 记为 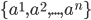 . 基于划分点
. 基于划分点 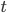 可将
可将  分为子集
分为子集 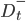 和
和 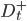 , 其中
, 其中 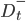 包含那些在属性
包含那些在属性  上取值不大于
上取值不大于 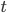 的样本, 而
的样本, 而 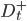 则包含那些在属性
则包含那些在属性  上取值大于
上取值大于 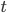 的样本. 显然, 对相邻的属性取值
的样本. 显然, 对相邻的属性取值 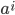 与
与 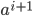 来说,
来说, 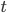 在区间
在区间 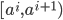 中任意取值所产生的划分结果相同. 因此, 对连续属性
中任意取值所产生的划分结果相同. 因此, 对连续属性  , 我们可考察包含
, 我们可考察包含 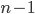 个元素的候选划分点集合:
个元素的候选划分点集合: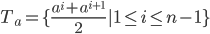
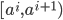 的中位点
的中位点 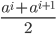 作为候选划分点. 然后我们就可以像离散属性值一样来考察这些划分点, 选取最优的划分点进行样本集合的划分. 对信息增益公式稍加改造则有:
作为候选划分点. 然后我们就可以像离散属性值一样来考察这些划分点, 选取最优的划分点进行样本集合的划分. 对信息增益公式稍加改造则有: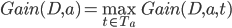
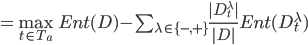 其中,
其中, 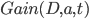 是样本集
是样本集  基于划分点
基于划分点 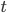 二分后的信息增益. 于是我们就可选择使
二分后的信息增益. 于是我们就可选择使 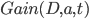 最大化的划分点.
最大化的划分点. 和属性
和属性  , 令
, 令 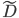 表示
表示  中在属性
中在属性  上没有缺失值的样本子集. 对问题1, 显然我们仅可根据
上没有缺失值的样本子集. 对问题1, 显然我们仅可根据 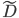 来判断属性
来判断属性  的优劣. 假定属性
的优劣. 假定属性  有
有 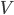 个可取值
个可取值 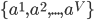 , 令
, 令 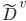 表示
表示 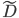 中在属性
中在属性  上取值为
上取值为 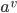 的样本子集,
的样本子集, 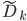 表示
表示 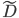 中属于第
中属于第 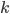 类
类 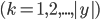 的样本子集, 则显然有
的样本子集, 则显然有 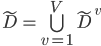 . 假定我们为每个样本
. 假定我们为每个样本  赋予一个权重
赋予一个权重 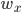 , 并定义:
, 并定义: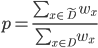
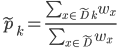
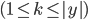
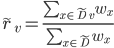
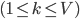
 ,
, 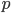 表示无缺失值样本所占的比例,
表示无缺失值样本所占的比例, 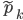 表示无缺失值样本中
表示无缺失值样本中 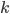 类所占的比例,
类所占的比例, 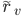 则表示无缺失值样本中在属性
则表示无缺失值样本中在属性  上取值
上取值 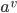 的样本所占的比例. 显然,
的样本所占的比例. 显然, 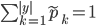 ,
, 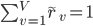 , 基于上述定义, 我们可将信息增益计算式推广为:
, 基于上述定义, 我们可将信息增益计算式推广为: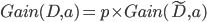
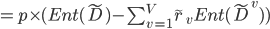
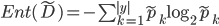
 在划分属性
在划分属性  上的取值已知, 则将
上的取值已知, 则将  划入与其取值对应的子结点, 且样本权值在子结点中保持为
划入与其取值对应的子结点, 且样本权值在子结点中保持为 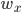 . 若样本
. 若样本  在划分属性
在划分属性  上的取值未知, 则将
上的取值未知, 则将  同时划入所有子结点, 且样本权值在于属性值
同时划入所有子结点, 且样本权值在于属性值 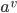 对应的子结点中调整为
对应的子结点中调整为 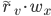 ; 直观的看, 这就是让同一个样本以不同的概率划入到不同的子结点中去.
; 直观的看, 这就是让同一个样本以不同的概率划入到不同的子结点中去.
Be First to Comment