Press "Enter" to skip to content
写在前面
- 今天我们继续学习类别不平衡问题, 本文中主要对处理类别不平衡问题的方法做了一定的介绍.
类别不平衡问题
- 前面介绍的分类学习方法都有一个通通的基本假设, 即不同类别的训练样例数目相当. 如果不同类别的训练样例数目稍有差别, 通常影响不大, 但若差别很大, 则会对学习过程造成困扰. 类别不平衡(Class-Imbalance)就是指分类任务中不同类别的训练样例数目差别很大的情况. 不失一般性, 本节假设正类样例较少, 反类样例较多. 在现实的分类学习任务中, 我们经常会遇到类别不平衡.
- 从线性分类器的角度讨论容易理解, 在我们用
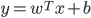 对新样本
对新样本  进行分类时, 事实上是在用预测出的
进行分类时, 事实上是在用预测出的 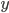 值与一个阈值进行比较. 例如通常在
值与一个阈值进行比较. 例如通常在 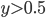 时判别为正例, 否则为反例.
时判别为正例, 否则为反例. 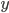 实际上表达了正例的可能性, 几率
实际上表达了正例的可能性, 几率 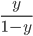 则反映了正例可能性与反例可能性之比值, 阈值设置为0.5恰表明分类器认为真实正, 反例可能性相同, 即分类器决策规则为: 若
则反映了正例可能性与反例可能性之比值, 阈值设置为0.5恰表明分类器认为真实正, 反例可能性相同, 即分类器决策规则为: 若 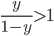 则预测为正例. 然而, 当训练集中正, 反例数目不同时, 令
则预测为正例. 然而, 当训练集中正, 反例数目不同时, 令 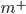 表示正例数目,
表示正例数目, 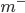 表示反例数目, 则观测几率是
表示反例数目, 则观测几率是 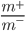 , 由于我们通常假设训练集是真实样本总体的无偏采样, 因此观测几率就代表了真实几率. 于是, 只要分类器的预测几率高于观测几率就判定为正例, 即: 若
, 由于我们通常假设训练集是真实样本总体的无偏采样, 因此观测几率就代表了真实几率. 于是, 只要分类器的预测几率高于观测几率就判定为正例, 即: 若 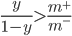 则预测为正例.
则预测为正例.
- 但是, 我们的分类器是基于: 若
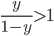 则预测为正例. 进行决策, 因此, 需对其预测值进行调整, 使其在决策时, 实际是在执行:
则预测为正例. 进行决策, 因此, 需对其预测值进行调整, 使其在决策时, 实际是在执行: 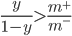 则预测为正例. 要做到这一点很容易, 只需令, 这事类别不平衡学习的一个基本策略--'再缩放'(Rescaling):
则预测为正例. 要做到这一点很容易, 只需令, 这事类别不平衡学习的一个基本策略--'再缩放'(Rescaling):
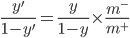
- 再缩放的思想虽简单, 但实际操作却并不平凡, 主要因为'训练集是真实样本总体的无偏采样'这个假设往往并不成立, 也就是说, 我们未必能有效地基于训练集观测几率来推断出真实几率. 现有技术大体上有三类做法:
- 第一类是直接对训练集里的反类样例进行'欠采样'(Undersampling), 即除去一些反例使得正反例数目接近, 然后再进行学习.
- 第二类是对训练集里的正类样例进行'过采样'(Oversampling), 即增加一些整理使得正反例数目接近, 然后再进行学习.
- 第三类则是直接基于原始训练集进行学习, 但在用训练好的分类器进行预测时, 将
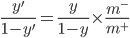 嵌入到其决策过程中, 称为'阈值移动'(Threshold-Moving).
嵌入到其决策过程中, 称为'阈值移动'(Threshold-Moving).
- 欠采样发的时间开销通常远小于过采样法, 因为前者丢弃了很多反例, 是的分类器训练集原小于初始训练集, 而过采样阀增加了很多正例, 其训练集大于初始训练集.
写在后面
- 在本文中, 我们介绍了如何使用欠采样/过采样的方法来对类别不平衡问题进行处理, 在实际生产环境中, 往往情况要更加的复杂, 理解好这些基础知识, 才能更加灵活的将其应用在生活与实际环境中.
- 明天, 我们将进入第四章-决策树, 并对决策树的基本流程, 划分选择进行介绍.
Related
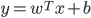 对新样本
对新样本  进行分类时, 事实上是在用预测出的
进行分类时, 事实上是在用预测出的 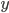 值与一个阈值进行比较. 例如通常在
值与一个阈值进行比较. 例如通常在 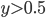 时判别为正例, 否则为反例.
时判别为正例, 否则为反例. 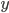 实际上表达了正例的可能性, 几率
实际上表达了正例的可能性, 几率 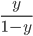 则反映了正例可能性与反例可能性之比值, 阈值设置为0.5恰表明分类器认为真实正, 反例可能性相同, 即分类器决策规则为: 若
则反映了正例可能性与反例可能性之比值, 阈值设置为0.5恰表明分类器认为真实正, 反例可能性相同, 即分类器决策规则为: 若 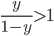 则预测为正例. 然而, 当训练集中正, 反例数目不同时, 令
则预测为正例. 然而, 当训练集中正, 反例数目不同时, 令 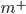 表示正例数目,
表示正例数目, 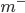 表示反例数目, 则观测几率是
表示反例数目, 则观测几率是 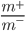 , 由于我们通常假设训练集是真实样本总体的无偏采样, 因此观测几率就代表了真实几率. 于是, 只要分类器的预测几率高于观测几率就判定为正例, 即: 若
, 由于我们通常假设训练集是真实样本总体的无偏采样, 因此观测几率就代表了真实几率. 于是, 只要分类器的预测几率高于观测几率就判定为正例, 即: 若 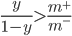 则预测为正例.
则预测为正例.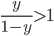 则预测为正例. 进行决策, 因此, 需对其预测值进行调整, 使其在决策时, 实际是在执行:
则预测为正例. 进行决策, 因此, 需对其预测值进行调整, 使其在决策时, 实际是在执行: 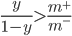 则预测为正例. 要做到这一点很容易, 只需令, 这事类别不平衡学习的一个基本策略--'再缩放'(Rescaling):
则预测为正例. 要做到这一点很容易, 只需令, 这事类别不平衡学习的一个基本策略--'再缩放'(Rescaling):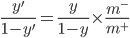
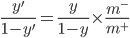 嵌入到其决策过程中, 称为'阈值移动'(Threshold-Moving).
嵌入到其决策过程中, 称为'阈值移动'(Threshold-Moving).
Be First to Comment