Press "Enter" to skip to content
写在前面
- 周志华老师的<机器学习>, 又被称为西瓜书, 每次读都会有一种耳目一新的感觉. 这次在微信公众号发起了西瓜书精读活动, 很多童鞋的需求都很强烈, 希望在我们一起努力下, 能对书中的知识有更深刻的认知.
- 机器学习是目前火热的人工智能领域中的一门大学科, 其中对高数, 线代, 统计学, 概率论的要求极高. 在看这个系列文章的同时, 如果遇见看不懂的公式或者名词, 可以适量的补充一些数学知识. 相信我们都会有所进步!
- 在这篇文章中, 我们对机器学习的基本概念与名词做了解释. 在学习完这个章节之后, 你会对机器学习有个大概的认知, 并且了解一些基本术语, 假设空间, 以及理解归纳偏好的概念.
引言
- 机器学习: 从数据产生'模型'(学习算法). 有了学习算法, 就能把经验(数据)提供给他, 他就能基于数据产生模型, 在面对新情况(数据)时, 模型会给我们提供相应的判断.
- 模型: 从数据中学得的结果.
- 模式: 局部性结果(例如, 一条规则).
基本术语
- 特征(Feature): 拿西瓜来举例的话, 色泽就是一个特征, 根蔕也是一个特征. 特征可以是一串文字, 一个形容词, 也可以是一个数字. 当然, 我们在处理的时候, 也可以将文字使用one-hot转换成数字, 再对某些特征经行统计, 分析.
- 数据集(DataSet): 数据集中包含很多条记录, 每条记录中包含很多个特征(Feature).
- 样本(Sample): 数据集中的某条记录.
- 样本空间(Sample Space): 某个样本张成的空间. (例如, 一个西瓜包含色泽, 根蔕, 敲声三个特征, 那么由这三个特征所张成的空间, 就叫做样本空间.), 一个样本也被称为一个特征向量(Feature Vector).
- 数学表述:
一个特征 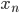
一个样本(第i个样本) 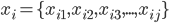
数据集 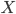
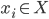
- 训练(Training): 训练在这里又被称为学习(Learning), 这个过程是通过执行某个学习算法来完成的.
- 训练集(Training Set): 训练集又被称为训练数据(Training Data), 其中每一个样本叫做训练样本(Training Sample).
- 验证集(Valid Set): 验证集, 主要用于验证训练出来模型的预测能力, 准确度, 错误率等.
- 训练集与验证集, 都来自数据集, 在后面的章节中, 会讲到如何将数据集按照比例划分为训练集与验证集.
- 假设(Hypothesis): 模型所学得的关于数据的某种潜在规律. 这种潜在规律自身, 则称为'真相'或'真实', 学习过程就是为了找出或逼近真相.
- 预测(Prediction): 通过模型对某个新数据进行预测.
- 标记(Label): 在训练的时候, 我们还需要获取数据集中对应的标签, 才能建立一个完整的关于'预测'的模型.
- 分类(Classification): 对于离散值的预测(例如, '好瓜', '坏瓜').
- 回归(Regression): 对于连续值的预测(例如, 成熟度, 0.95, 0.37).
- 二分类(Binary Classification)任务: 通常称其中一个类为'正类'(Positive Class), 另一个类为'反类'(Negative Class).
- 多分类(Multi-Class Classification)任务: 预测任务希望通过对训练集
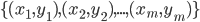 进行学习, 简历一个从输入空间
进行学习, 简历一个从输入空间 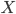 到输出空间
到输出空间 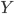 的映射
的映射 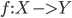 . 对二分类任务, 通常令
. 对二分类任务, 通常令 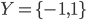 或
或 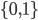 ; 对多分类任务,
; 对多分类任务, 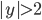 ; 对回归任务,
; 对回归任务, 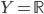 ,
, 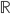 为实数集.
为实数集.
- 测试(Testing): 学的模型后, 使用其进行预测的过程称为'测试'(Testing), 被预测的样本被称为'测试样本'(Testing Sample). 例如, 在学得
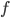 后, 对测试例
后, 对测试例  , 可得到其预测标记
, 可得到其预测标记 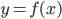 .
.
- 聚类(Clusting): 将训练集中的西瓜分成若干组, 每组称为一个'簇'(Cluster); 这些自动形成的'簇'可能对应一些潜在的概念划分. 例如, '浅色瓜', '深色瓜'. 这样的学习过程有助于我们了解数据内在的规律, 能更深入的分析数据建立基础. 需说明的是, 在聚类学习中, '浅色瓜', '深色瓜', 这样的概念我们事先是不知道的, 而且学习过程中使用的训练样本通常不拥有标记(Label)信息.
- 监督学习(Supervised Learning): 分类, 回归.
- 无监督学习(Unsupervised Learning): 聚类.
- 泛化(Generalization)能力: 学的模型适用于新样本的能力.
- 分布(Distribution): 通常假设样本空间中全体样本服从一个未知'分布'(Distribution)
 , 我们获得的每个样本都是独立地从这个分布上采样获得的, 即'独立同分布'(Independent and Indentically Distributed, 简称i.i.d). 一般而言, 训练样本越多, 我们得到的关于
, 我们获得的每个样本都是独立地从这个分布上采样获得的, 即'独立同分布'(Independent and Indentically Distributed, 简称i.i.d). 一般而言, 训练样本越多, 我们得到的关于  的信息越多, 这样就有可能通过学习获得具有强泛化能力的模型.
的信息越多, 这样就有可能通过学习获得具有强泛化能力的模型.
假设空间
- 归纳(Induction)与演绎(Deduction)是科学推理的两大基本手段. 前者是从特殊到一般的'泛化'(Generalization)过程, 即从具体的事实归结出一般性规律; 后者则是从一般到特殊的'特化'(Specialization)过程, 即从基础原理推演出具体状况. '从样本中学习'显然是一个归纳的过程, 因此也被称为'归纳学习'(Inductive Learning).
- 归纳学习有狭义与广义之分, 广义的归纳学习大体相当于从样例中学习, 而狭义的归纳学习则要求从训练数据中学的概念(concept), 因此也被称作为'概念学习'或'概念形成'. 概念学习技术目前研究, 应用领域都比较少, 因为要学得泛化性能好且予以明确的概念实在太困难了, 限时常用的技术大多是产生'黑箱'模型.
- 我们可以把学习过程看做一个在所有假设(Hypothesis)组成的空间中进行搜索的过程, 搜索目标是找到与训练集'匹配'(Fit)的假设, 即能够将训练集中的瓜判断正确的假设. 假设的表示一旦确定, 假设空间及其规模大小就确定了.
归纳偏好
- 任何一个有效的机器学习算法必有其归纳偏好, 否则它将被假设空间中看似在训练集上'等效'的假设所迷惑, 而无法产生确定的学习结果. 可以想象, 如果没有偏好, 我们的西瓜学习算法产生的模型每次在进行与测试随机抽选训练集上的等效假设, 那么对新输入数据, 学的模型时而告诉我们它是好的, 时而告诉我们它是不好的, 这样的学习结果显然没有意义.
- 归纳偏好可以看做学习算法自身在一个可能很庞大的假设空间中对假设进行选择的启发式或'价值观'. 那么, 有没有一般性的原则来引导算法确立'正确的'偏好呢? '奥卡姆剃刀'(Occam's razor)是一种常用的, 自然科学研究中最基本的原则.
- 奥卡姆剃刀(OCcam's razor)原则: 如有多个假设与观察一致, 则选最简单的那个.
- 然而, 奥卡姆剃刀并非唯一可行的原则, 退一步说, 即使我们是奥卡姆剃刀的铁杆拥趸, 也需要注意到, 奥卡姆剃刀本身存在不同的诠释, 使用奥卡姆剃刀原则并不平凡.
- 事实上, 归纳偏好对应了学习算法本身所作出的关于'什么样的模型更好'的假设. 在具体的现实问题中, 这个假设是否成立, 即算法的归纳偏好是否与问题本身匹配, 大多数时候直接决定了算法能否取得好的性能.
写在后面
- 在这篇文章中, 大致总结了绪论中的一些比较重要的知识点, 后面还有些发展历程和应用现状, 看看书了解下就好了.
- 明天, 我们将继续学习下一个章节--模型评估与选择.
Related
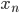
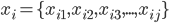
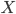
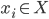
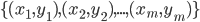 进行学习, 简历一个从输入空间
进行学习, 简历一个从输入空间 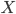 到输出空间
到输出空间 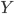 的映射
的映射 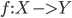 . 对二分类任务, 通常令
. 对二分类任务, 通常令 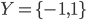 或
或 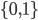 ; 对多分类任务,
; 对多分类任务, 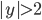 ; 对回归任务,
; 对回归任务, 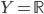 ,
, 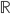 为实数集.
为实数集.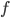 后, 对测试例
后, 对测试例  , 可得到其预测标记
, 可得到其预测标记 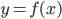 .
. , 我们获得的每个样本都是独立地从这个分布上采样获得的, 即'独立同分布'(Independent and Indentically Distributed, 简称i.i.d). 一般而言, 训练样本越多, 我们得到的关于
, 我们获得的每个样本都是独立地从这个分布上采样获得的, 即'独立同分布'(Independent and Indentically Distributed, 简称i.i.d). 一般而言, 训练样本越多, 我们得到的关于  的信息越多, 这样就有可能通过学习获得具有强泛化能力的模型.
的信息越多, 这样就有可能通过学习获得具有强泛化能力的模型.
写的很用心,谢谢楼主。