Press "Enter" to skip to content
写在前面
- 在这篇文章中, 将会用图例的方式来对一些常用的求导公式进行讲解, 以便于对微积分概念的理解.
关于 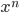
- 我们先从
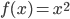 开始理解.
开始理解.
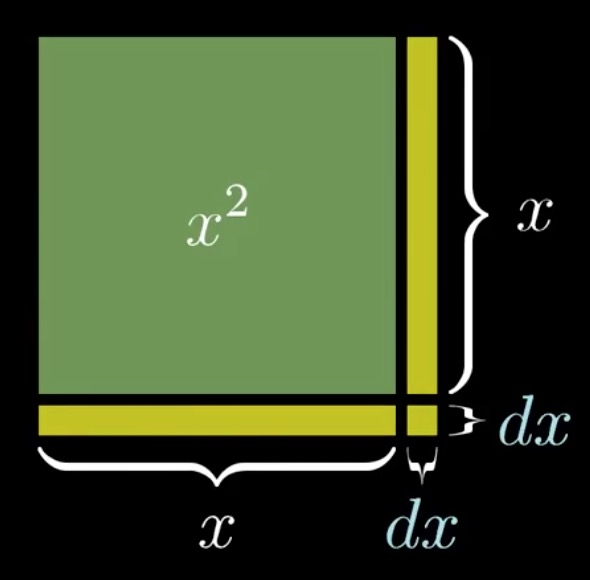
- 如图, 假设我们要在
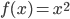 上增加一个微量
上增加一个微量 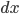 (其实这里就是对
(其实这里就是对 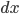 求导), 那会增加图中黄色矩形部分面积.
求导), 那会增加图中黄色矩形部分面积.
- 我们暂且叫这个部分增加的面积为df, 那么计算一下黄色矩形部分的面积:
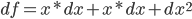
- 由于
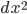 非常小, 试想, 假设
非常小, 试想, 假设 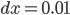 , 则有
, 则有 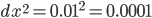 , 对我们整体数据的影响是非常小的, 所以可以忽略这部分的值不计, 最后得出
, 对我们整体数据的影响是非常小的, 所以可以忽略这部分的值不计, 最后得出 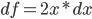
- 得出
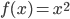 的导数:
的导数: 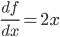
- 然后我们接下来看看
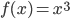 .
.
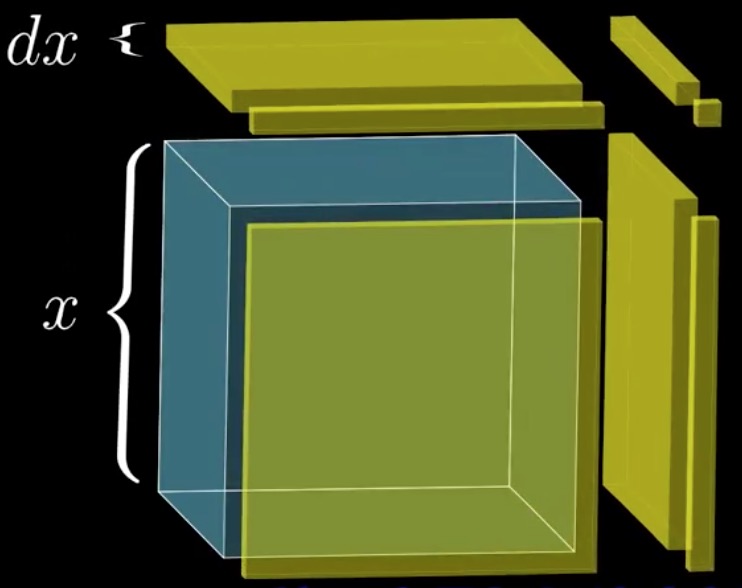
- 同样的, 假设我们要在
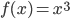 上增加一个微量
上增加一个微量 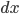 , 会增加图中黄色部分面积.
, 会增加图中黄色部分面积.
- 则有:
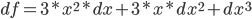
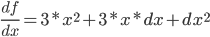
- 忽略非常小的
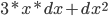 后得到
后得到 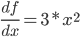 .
.
- 当
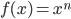 时, 新的函数值为:
时, 新的函数值为:
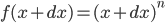
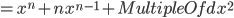
- 忽略这些非常小的
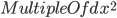 , 最后得到
, 最后得到 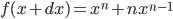 ,
, 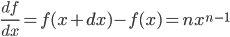 .
.
- 抽象的说,
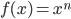 中, 无论n是多少,
中, 无论n是多少, 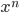 的导数都为
的导数都为 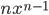 .
.
- 最后得到幂函数求导公式:
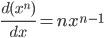
关于 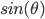
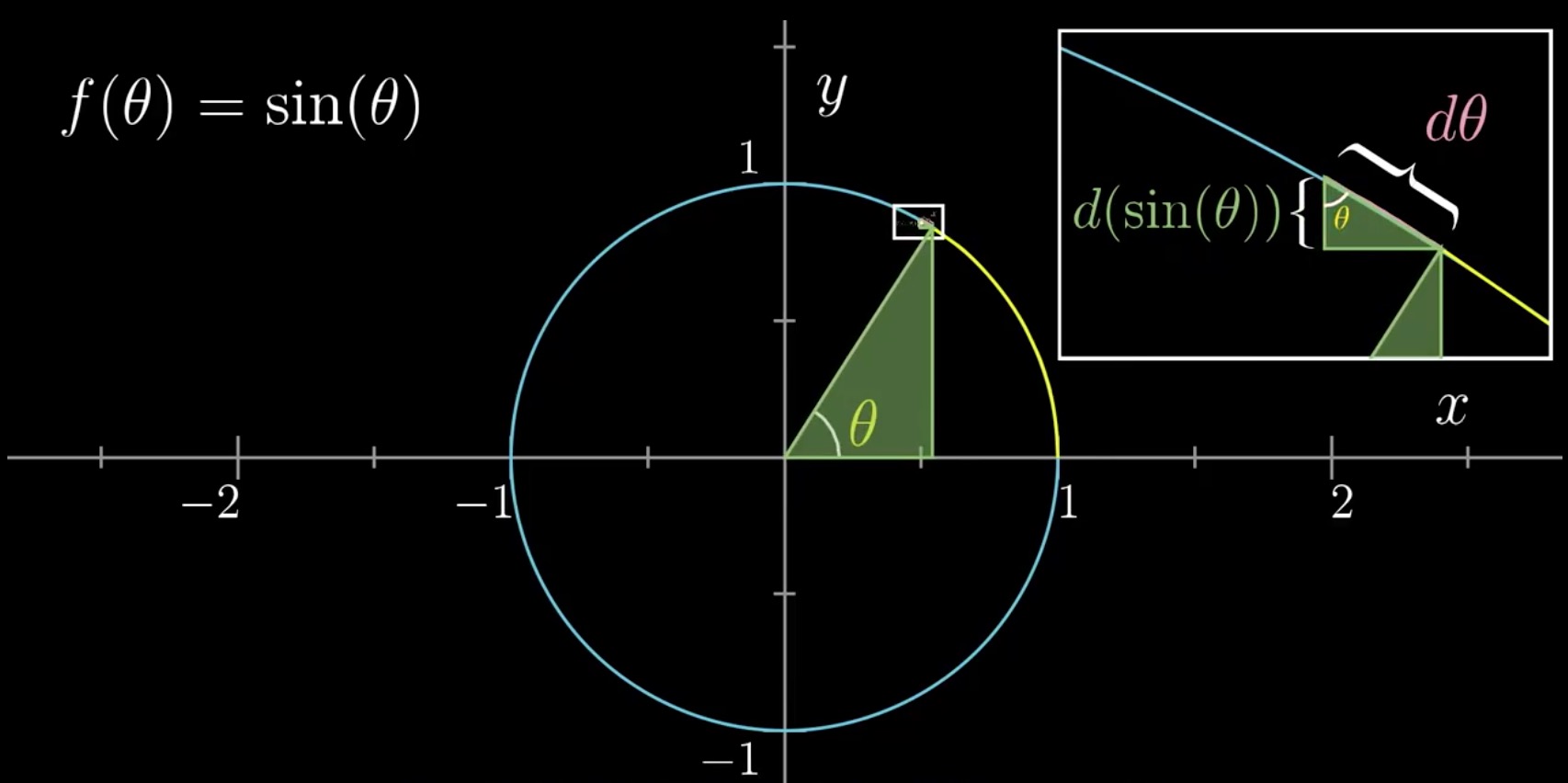
- 如图, 假设我们要在
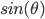 上增加一个微量
上增加一个微量 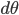 , 并已知小直角三角形与大直角三角形相似.
, 并已知小直角三角形与大直角三角形相似.
- 则有
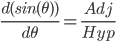 (就是临边比斜边), 不正是
(就是临边比斜边), 不正是 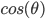 吗.
吗.
- 最后得到结论:
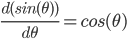
一些常用的求导公式
写在最后
- 这章详细介绍了
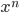 ,
, 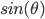 用图形求解的方法, 并熟悉了些比较常用的求导公式.
用图形求解的方法, 并熟悉了些比较常用的求导公式.
- 在下一章中, 我们将主要探讨, 函数求和, 乘积, 复合函数.
Related
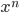
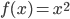 开始理解.
开始理解.
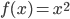 上增加一个微量
上增加一个微量 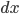 (其实这里就是对
(其实这里就是对 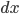 求导), 那会增加图中黄色矩形部分面积.
求导), 那会增加图中黄色矩形部分面积.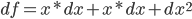
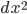 非常小, 试想, 假设
非常小, 试想, 假设 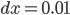 , 则有
, 则有 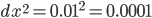 , 对我们整体数据的影响是非常小的, 所以可以忽略这部分的值不计, 最后得出
, 对我们整体数据的影响是非常小的, 所以可以忽略这部分的值不计, 最后得出 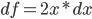
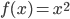 的导数:
的导数: 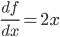
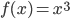 .
.
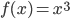 上增加一个微量
上增加一个微量 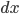 , 会增加图中黄色部分面积.
, 会增加图中黄色部分面积.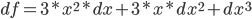
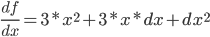
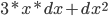 后得到
后得到 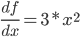 .
.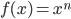 时, 新的函数值为:
时, 新的函数值为: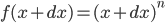
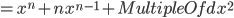
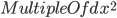 , 最后得到
, 最后得到 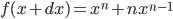 ,
, 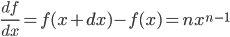 .
.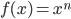 中, 无论n是多少,
中, 无论n是多少, 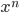 的导数都为
的导数都为 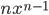 .
.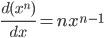
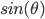

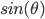 上增加一个微量
上增加一个微量 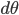 , 并已知小直角三角形与大直角三角形相似.
, 并已知小直角三角形与大直角三角形相似.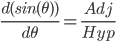 (就是临边比斜边), 不正是
(就是临边比斜边), 不正是 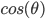 吗.
吗.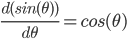
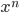 ,
, 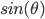 用图形求解的方法, 并熟悉了些比较常用的求导公式.
用图形求解的方法, 并熟悉了些比较常用的求导公式.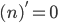
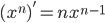
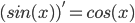
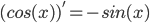
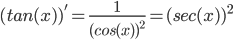
Be First to Comment