写在前面
- 这里开始补充一些机器学习中所会经常接触到的微积分知识.
- 最近在看B站本质系列, 链接贴一下微积分的本质 - 01, 有兴趣的童鞋也可以去看看, 讲得很基础.
关于圆的面积

对于圆的面积的算法一开始我们并不清晰, 如果用微积分的思路, 将其分为多个微小的同心圆, 则可将其展开. 下图为一个宽度非常小的同心圆(当然, 这里为了方便查看与学习, 将其放大了.), 将其从原型中抽离出来的模样.

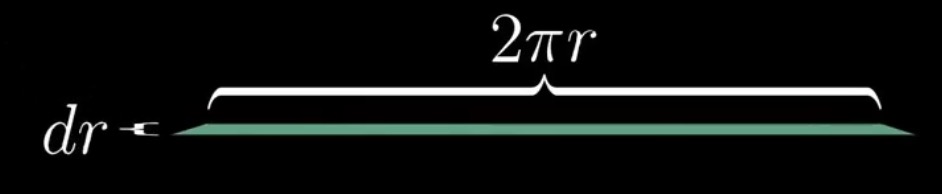
将它拉直了之后, 可以近似的看成是一个长方形.

我们假设这个长方形的宽度是dr, 这里的dr如果取值越小, 划分越细, 就越接近与圆的真实面积. 已知圆的周长是可以用 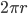 来计算的, 那么就得到下图.
来计算的, 那么就得到下图.
这样我们就可以计算每个空心圆的面积 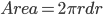 . 将这些同心的空心圆展开后放在坐标轴中, 并绘制相应的周长函数(那条直线).
. 将这些同心的空心圆展开后放在坐标轴中, 并绘制相应的周长函数(那条直线).
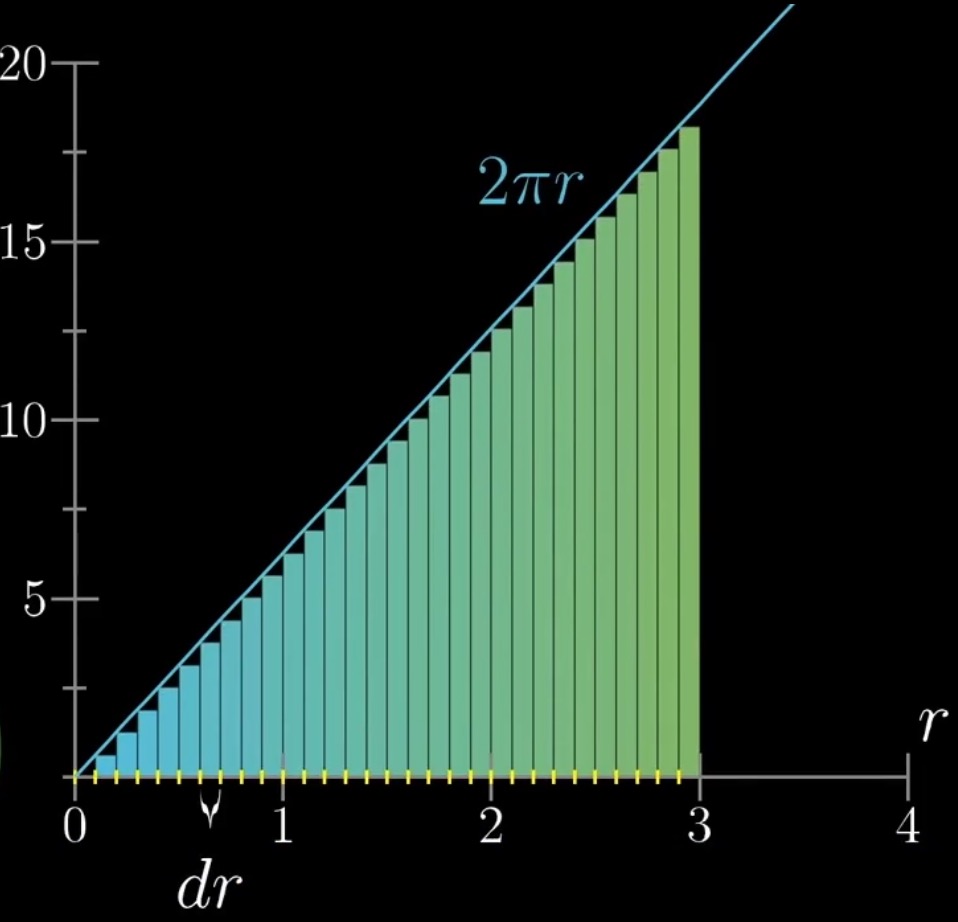
可以发现, 只要当dr取值足够小时, 就可以通过微积分的方法近似算出圆形的面积. 注意, 我们这里是在做近似.
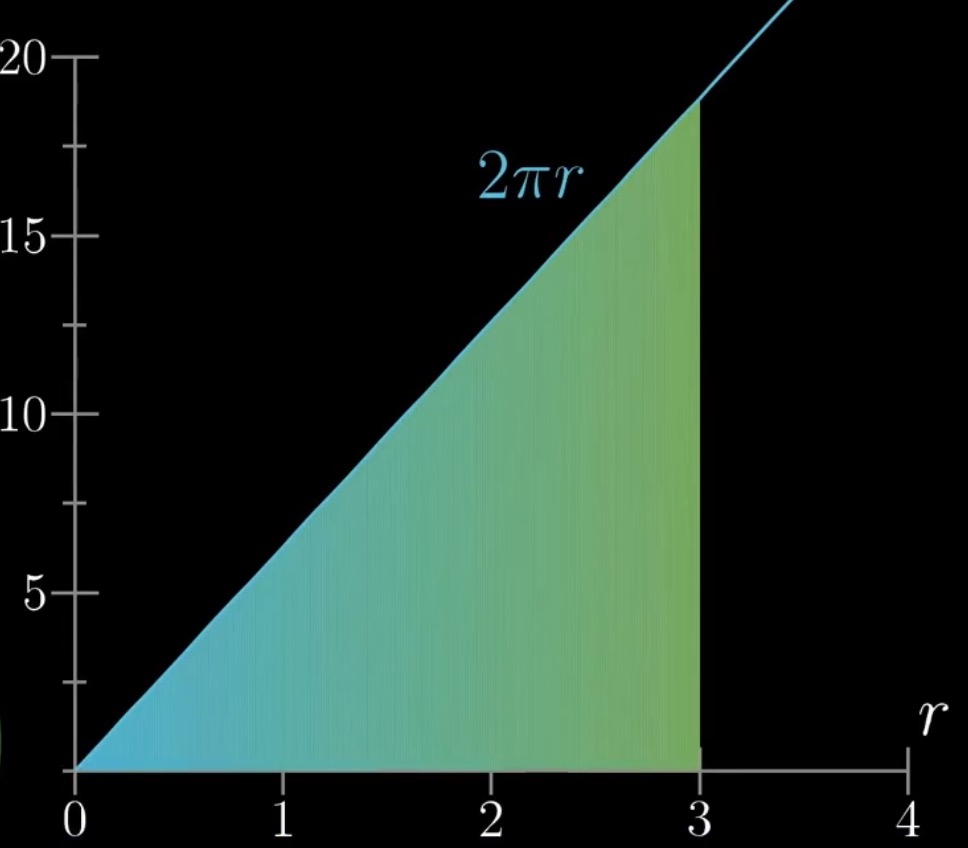
不难发现, 我们需要求的圆形面积, 就是底下这个三角形的面积.
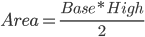
在这里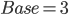 ,
, 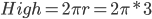 , 那么可以得出
, 那么可以得出 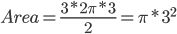
当然这个在所有的圆形面积计算中都会奏效, 假设圆形半径为R, 则圆形面积则为 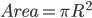
解决难题的思路
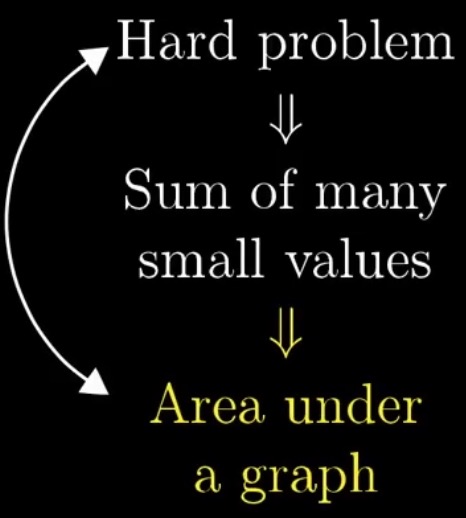
- 当一个难题难以解决时, 尝试将其划分为多个微小的值, 先去求原问题的近似.
积分
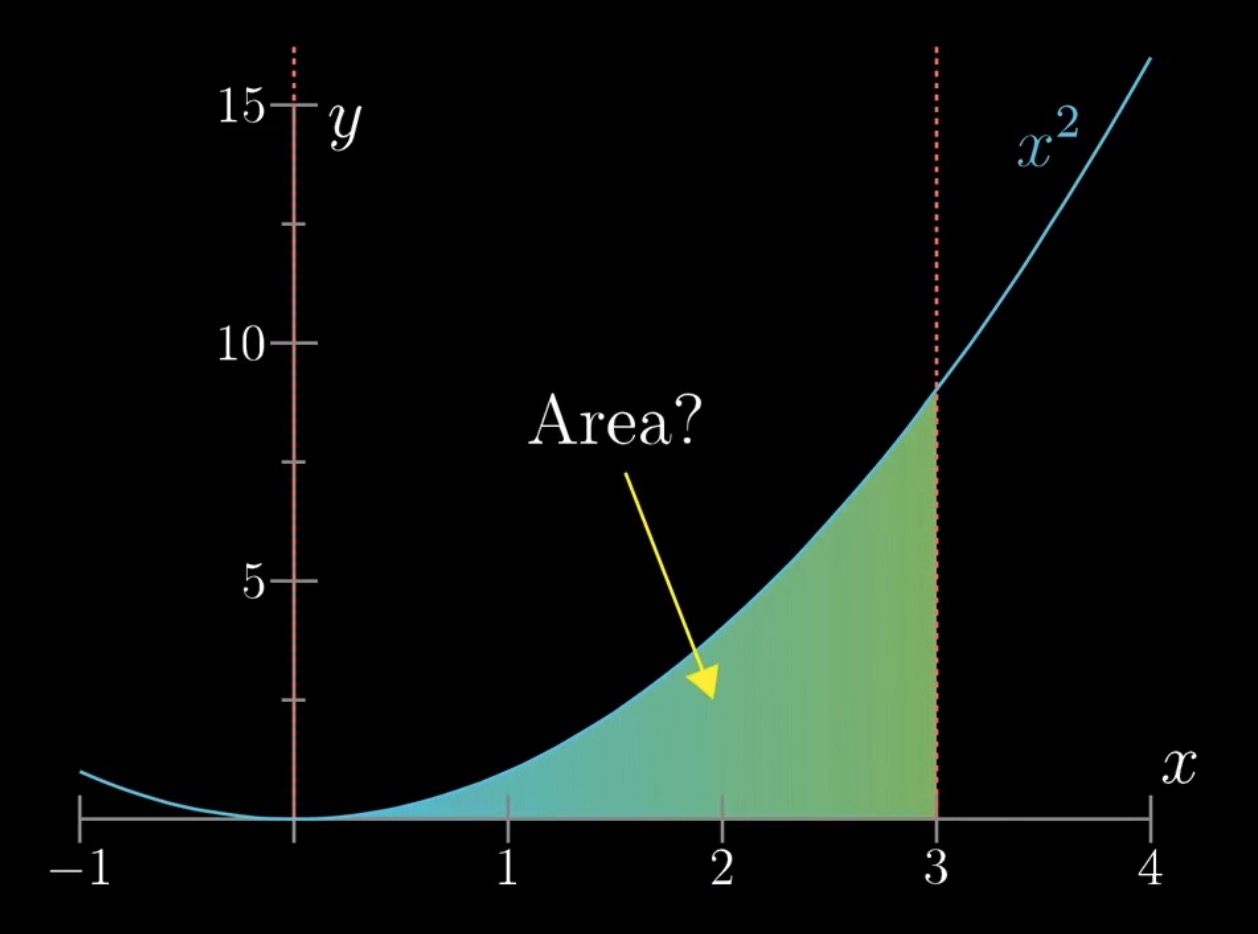
找到一个可以表示这个Area大小变化的函数.
导数
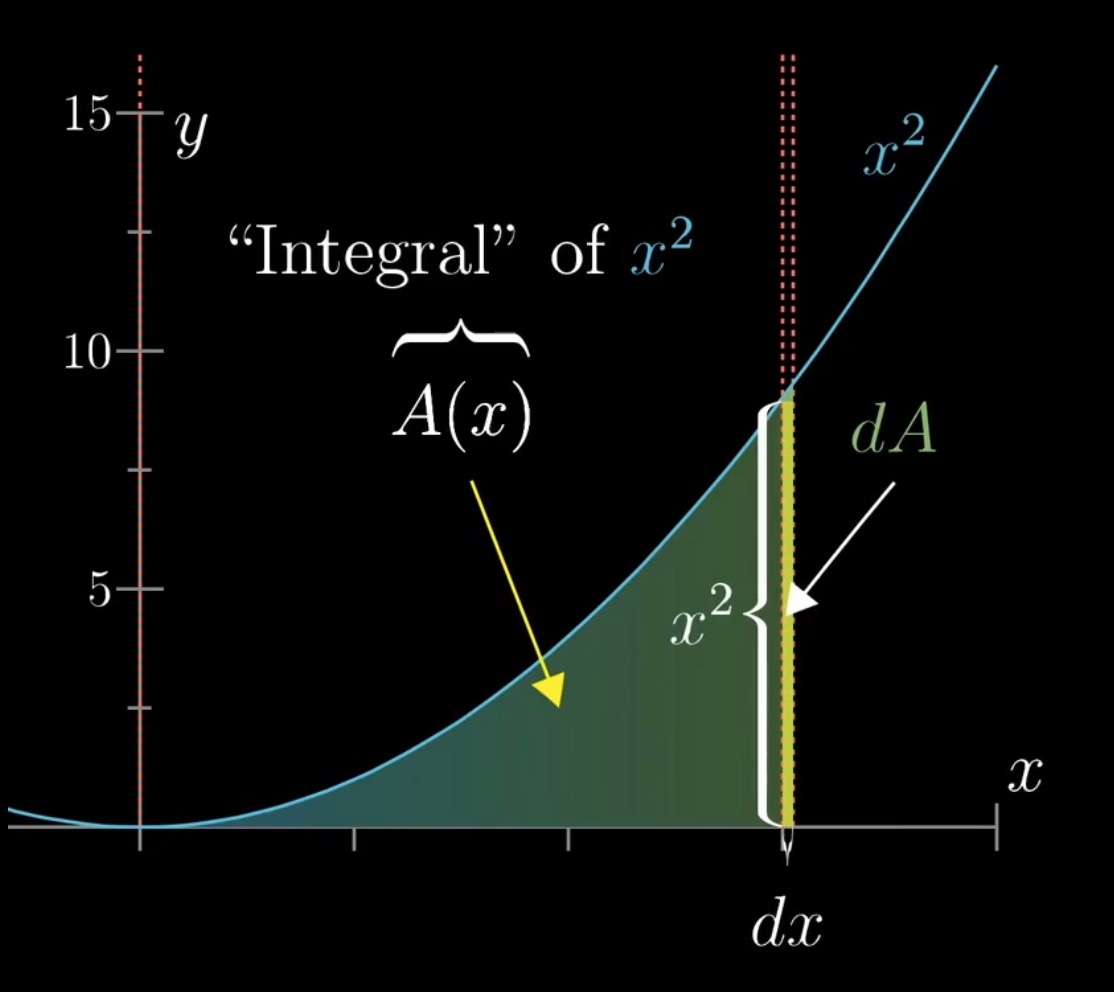
假设 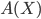 就是可以表示这个Area大小变化的函数. 如图, 假设
就是可以表示这个Area大小变化的函数. 如图, 假设 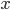 轴发生了细微的变化
轴发生了细微的变化 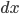 , 将此部分近似看成长方形, 则此部分面积表示为
, 将此部分近似看成长方形, 则此部分面积表示为 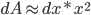 . 将
. 将 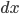 放到等式的左边, 则推导出
放到等式的左边, 则推导出 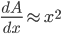 . 在这里
. 在这里 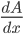 叫做A的导数, 是当
叫做A的导数, 是当 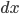 越来越小时, 这个比值趋向的值.
越来越小时, 这个比值趋向的值.
写在最后
- 在这个章节中, 我们认识了积分与导数, 以及一些基本的推导过程和解决难题的方法, 这些方法不仅仅可以运用在数学领域, 还被充分的运用在多个领域, 是我们值得深思与研究的. 当然, 现实中的问题, 也会更加的复杂.
Be First to Comment