写在前面
在这章内容中, 将重点探讨决策树的表述方式, ID3, 以及如何处理连续属性, 何时停止等问题.
分类与回归
Classification(分类): 将输入的值映射到离散值.
Regression(回归): 从某种输入空间映射到某个实际数字.
分类学习
- Instance(实例): 输入集, 可以是相片, 评分等数据.
- Concept(概念): 函数, 将输入映射到输出, 提取实例信息, 将实例映射到某类输出(True|False).
- Target Concept(目标概念): 实际答案.
- Hyprhesis(假设): 所有概念的集合, 所有可能的函数.
- Sample(样本): 训练集.
- Candindate(候选者): 一个你认可可能会是目标概念的概念.
- Testing Set(测试集): 测试集.
决策树学习
- 挑选最佳属性.
- 提出一个相关问题.
- 沿着答案的路径.
- 然后继续挑选最佳属性, 反复以上步骤, 直至可能性空间缩小到只有一个答案的时候停止.
可表达性
AND
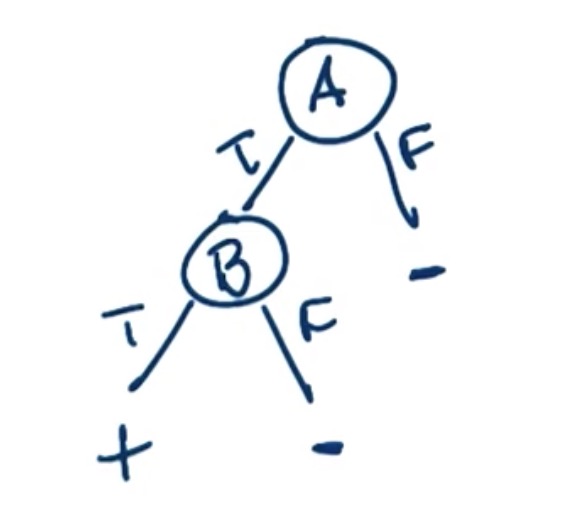
如图, 决策树可以通过两个节点表述A AND B的计算过程与结果.
OR
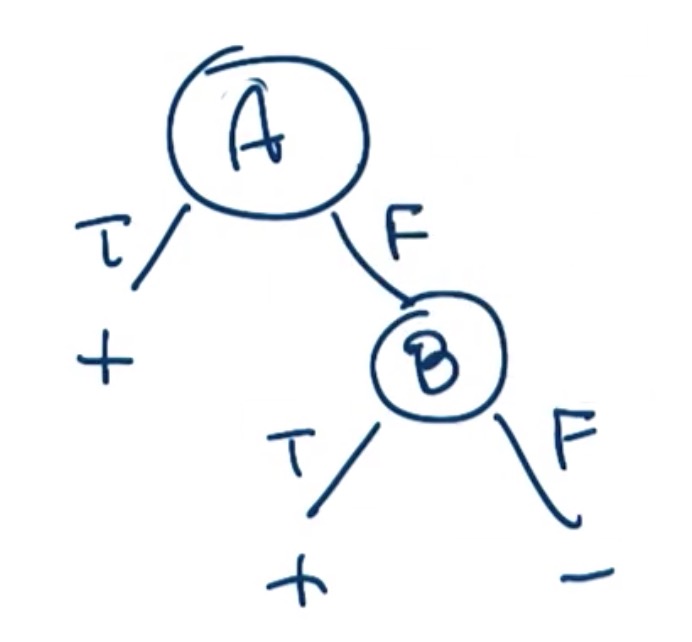
如图, 决策树可以通过两个节点表述A OR B的计算过程与结果.
XOR
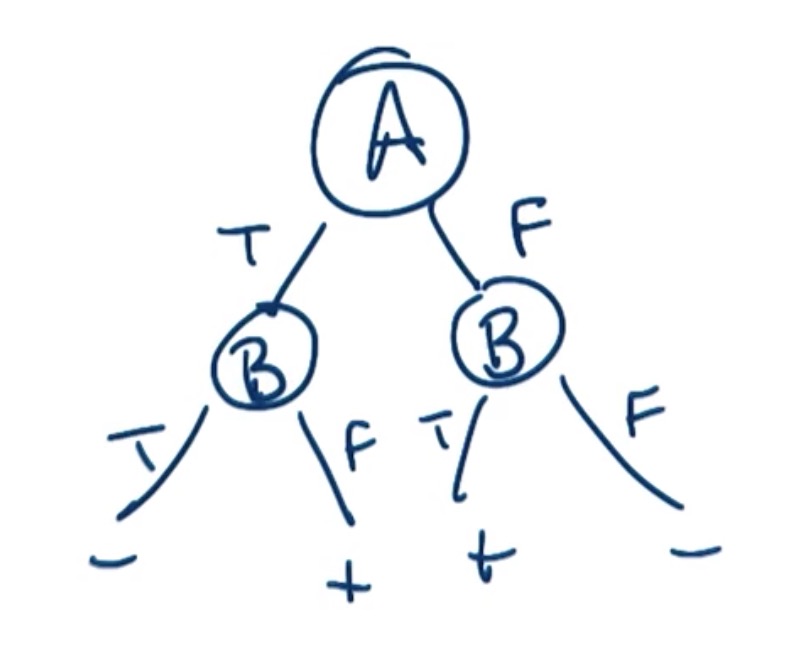
如图, 决策树可以通过两个节点表述A XOR B的计算过程与结果.
ID3算法
- 选取A作为最优属性分割数据
- 分配A作为节点的决策属性
- 为A的每个值创建一个决策节点
- 将训练实例分类到叶子
- 如果训练集完美分类则停止, 否则继续迭代
ID3偏差
- Restriction Bias(限定偏差): Hyprhesis(假设)集合, 决策树以及它可以表述的内容, 而不会去考虑一元二次函数以及无穷函数等, 只考虑决策树中所给出的离散变量所表示的可能情况.
- Reference Bias(优选偏差): 它会告诉我们首选的假设集合的来源.
- 归纳偏差: ID3算法的归纳偏差来自它的搜索策略, 该策略假定某种假设胜于其它假设, 较短的假设比较长的假设要更优, 因此称这种归纳偏差为优选偏差或搜索偏差. 相反, 候选消除算法的偏差是对待考虑假设的一种限定, 这种形式的偏差通常称为限定偏差或语言偏差. 通常, 优选偏置比限定偏置更符合需要. 因为它保证了位置的目标函数被包含在学习器工作的假设空间中(要不然很可能白忙活一场). 但在实际中, 综合使用两者的学习系统是很常见的(例如使用最小均方差(优选偏置)的以线性函数(限定偏置)来表示评估函数的问题).
处理连续属性
使用决策树处理决策属性时, 可以采用范围判断的方式.(注意有效的范围选取)
例如: 年龄可以分为>=20|<20两部分, 这样就可以对一些连续的数值进行处理, 例如输入18.5, 则被归类到<20这部分.
什么时候停止
- 内容被正确归类时.(如果有多个对象相同, 实例相同, 但标签不同的样本, 则会陷入死循环.)
- 属性耗尽时.(对于连续属性的处理不好)
- 注意overfit(过拟合).(根据交叉验证和测试集来检查决策树)
- 剪枝.(会出现误差)
写在最后
到这里, 对决策树的概念及算法已经有了大致的认识. 接下来还会陆续更新一些细节相关的内容.
Be First to Comment