关于信息增益计算
Informatio_Gain = Entropy(parent) - [weighted_average] * Entropy(children)
现有数据集
| Grade | Bumpiness | Speed_Limit? | Speed |
|---|---|---|---|
| steep | bumpy | yes | slow |
| steep | smooth | yes | slow |
| flat | bumpy | no | fast |
| steep | smooth | no | fast |
计算Entropy(parent)的熵
在这个数据集中, parent为Speed, 我们需要计算Entropy(parent)的值.
关于熵的计算, 请查看此链接Entropy.
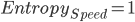
计算Grade的权重
| Grade | Bumpiness | Speed_Limit? | Speed |
|---|---|---|---|
| steep | bumpy | yes | slow |
| steep | smooth | yes | slow |
| flat | bumpy | no | fast |
| steep | smooth | no | fast |
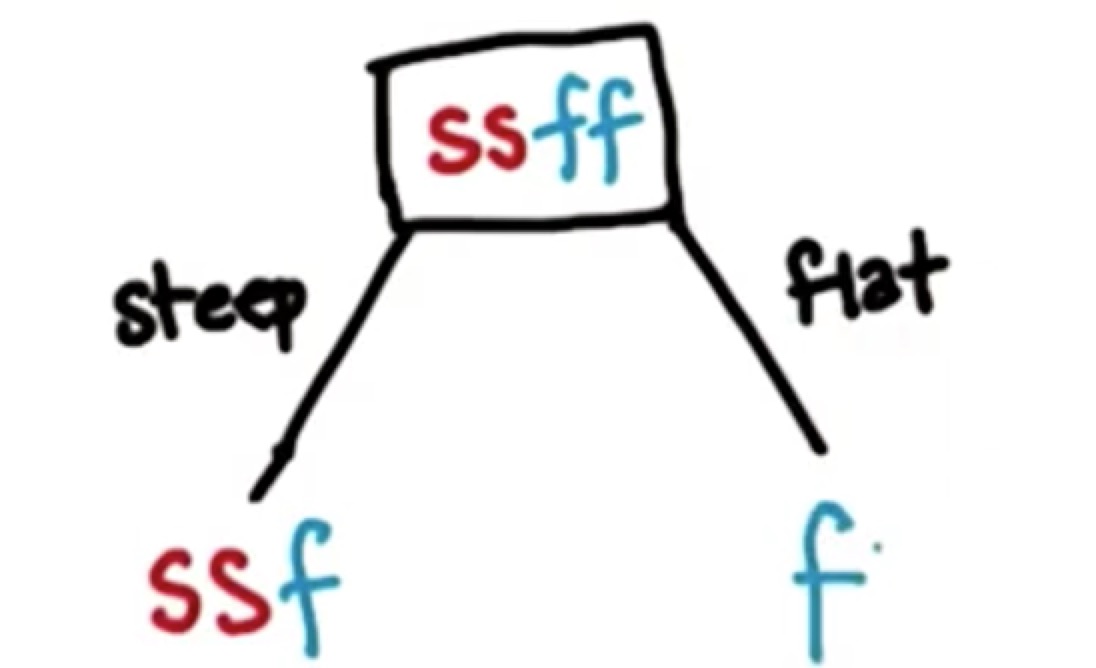
- 如图所示, 我们在第一步已经用决策树将Speed分为slow和fast两个分支.
- 将分成两个分支, 分支为值为steep的行; 第二分支为值为flat的行. 分别计算这两个部分的权重值.
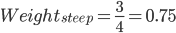
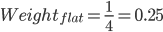
计算分支的熵
- 我们先计算左侧分支[ssf]的熵
手动统计概率:
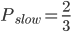
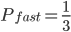
用Python实现, 并存入List, 便于计算:
plist = [2 / 3, 1 / 3]
将其带入Entropy()得到答案:
➜ test ✗ python3 entropy.py 0.9182958340544896
后面计算时, 取小数点后四位, 四舍五入, 0.9183.
- 接着计算右侧分支[s]的熵
手动统计概率:
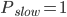
plist = [1]
将其带入Entropy()得到答案:
➜ test ✗ python3 entropy.py 0.0
[weighted_average] * Entropy(children)计算
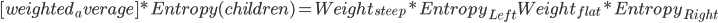
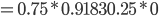
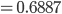
Information_Gain
Information_Gain = Entropy(parent) - [weighted_average] * Entropy(children)
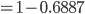
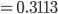
Be First to Comment