Press "Enter" to skip to content
写在前面
- 昨天, 我们学习了聚类中的聚类任务; 今天, 我们将继续学习聚类中的性能度量.
性能度量
- 聚类性能度量亦称聚类'有效性指标'(Validity Index). 与监督学习中的性能度量作用相似, 对类似结果, 我们需通过某种性能度量来评估其好坏; 另一方面, 若明确了最终将要使用的性能度量, 则可直接将其作为聚类过程的优化目标, 从而更好地得到符号要求的聚类结果.
- 聚类是将样本集
 划分为若干互不相交的子集, 即样本簇. 那么, 什么样的聚类结果比较好呢? 直观上看, 我们希望'物以类聚', 即同一簇的样本尽可能彼此相似, 不同簇的样本尽可能不同. 换言之, 聚类结果的'簇内相似度'(Intra-Cluster Similarity)高且'簇间相似度'(Inter-Cluster Similarity)低.
划分为若干互不相交的子集, 即样本簇. 那么, 什么样的聚类结果比较好呢? 直观上看, 我们希望'物以类聚', 即同一簇的样本尽可能彼此相似, 不同簇的样本尽可能不同. 换言之, 聚类结果的'簇内相似度'(Intra-Cluster Similarity)高且'簇间相似度'(Inter-Cluster Similarity)低.
- 聚类性能度量大致有两类. 一类是将聚类结果与某个'参考模型'(Reference Model)进行比较, 称为'外部指标'(External Index); 另一类是直接考察聚类结果而不利用任何参考模型, 称为'内部指标'(Internal Index).
- 对数据集
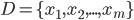 , 假定通过聚类给出的簇划分为
, 假定通过聚类给出的簇划分为 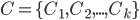 . 相应地, 令
. 相应地, 令 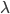 与
与 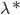 分别表示与
分别表示与 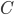 和
和 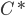 对应的簇标记向量. 我们将样本两两配对考虑, 定义:
对应的簇标记向量. 我们将样本两两配对考虑, 定义:
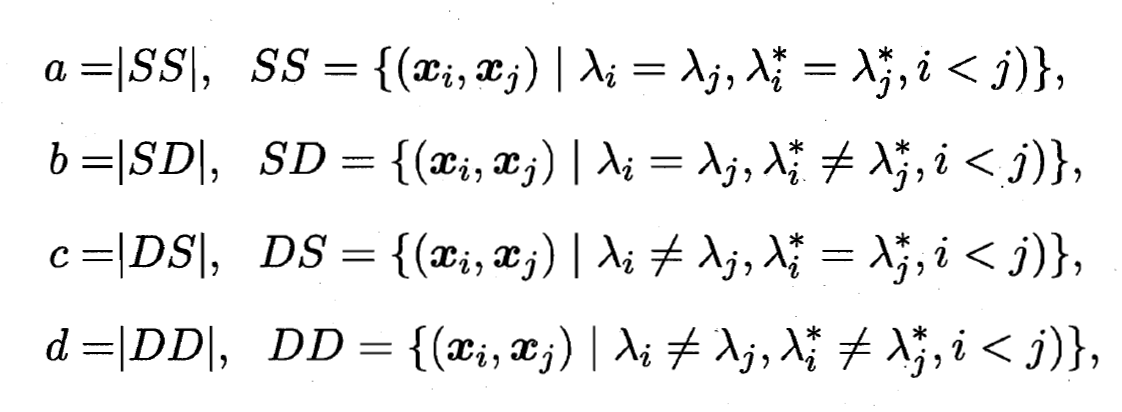
- 其中集合
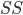 包含了在
包含了在 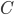 中隶属于相同簇且在
中隶属于相同簇且在 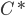 中也隶属于相同簇的样本对, 集合
中也隶属于相同簇的样本对, 集合 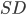 包含了在
包含了在 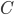 中隶属于相同簇但在
中隶属于相同簇但在 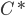 中隶属于不同簇的样本对, 由于每个样本对
中隶属于不同簇的样本对, 由于每个样本对 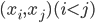 仅能出现在一个集合中, 因此有
仅能出现在一个集合中, 因此有 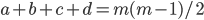 成立. 则有:
成立. 则有:


- 显然, 上述性能度量的结果值均在
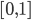 区间, 值越大越好. 考虑聚类结果的簇划分
区间, 值越大越好. 考虑聚类结果的簇划分 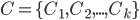 , 定义:
, 定义:
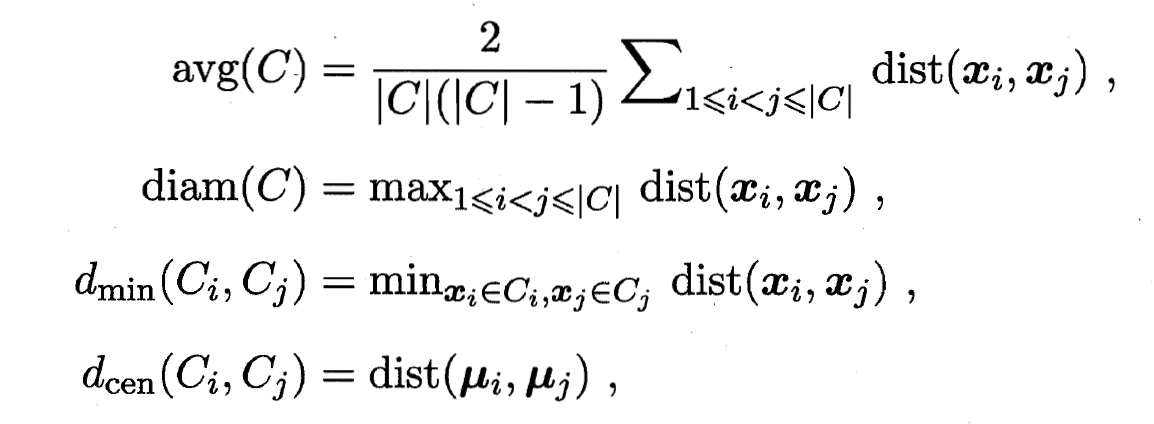
- 其中,
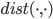 用于计算两个样本之间的距离;
用于计算两个样本之间的距离; 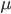 代表簇
代表簇 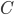 的中心点
的中心点 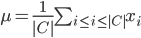 . 显然,
. 显然, 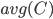 对应于簇
对应于簇 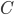 内样本间的平均距离,
内样本间的平均距离, 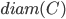 对应于簇
对应于簇 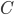 内样本间的最远距离,
内样本间的最远距离, 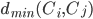 对应于簇
对应于簇 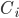 与簇
与簇 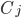 最近样本间的距离,
最近样本间的距离, 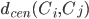 对应于簇
对应于簇 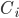 与簇
与簇 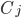 中心点检的距离, 则有:
中心点检的距离, 则有:

写在后面
- 今天, 我们学习了聚类中的性能度量; 明天, 我们将继续学习聚类中的距离计算.
 划分为若干互不相交的子集, 即样本簇. 那么, 什么样的聚类结果比较好呢? 直观上看, 我们希望'物以类聚', 即同一簇的样本尽可能彼此相似, 不同簇的样本尽可能不同. 换言之, 聚类结果的'簇内相似度'(Intra-Cluster Similarity)高且'簇间相似度'(Inter-Cluster Similarity)低.
划分为若干互不相交的子集, 即样本簇. 那么, 什么样的聚类结果比较好呢? 直观上看, 我们希望'物以类聚', 即同一簇的样本尽可能彼此相似, 不同簇的样本尽可能不同. 换言之, 聚类结果的'簇内相似度'(Intra-Cluster Similarity)高且'簇间相似度'(Inter-Cluster Similarity)低.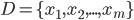 , 假定通过聚类给出的簇划分为
, 假定通过聚类给出的簇划分为 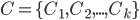 . 相应地, 令
. 相应地, 令 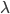 与
与 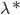 分别表示与
分别表示与 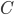 和
和 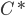 对应的簇标记向量. 我们将样本两两配对考虑, 定义:
对应的簇标记向量. 我们将样本两两配对考虑, 定义: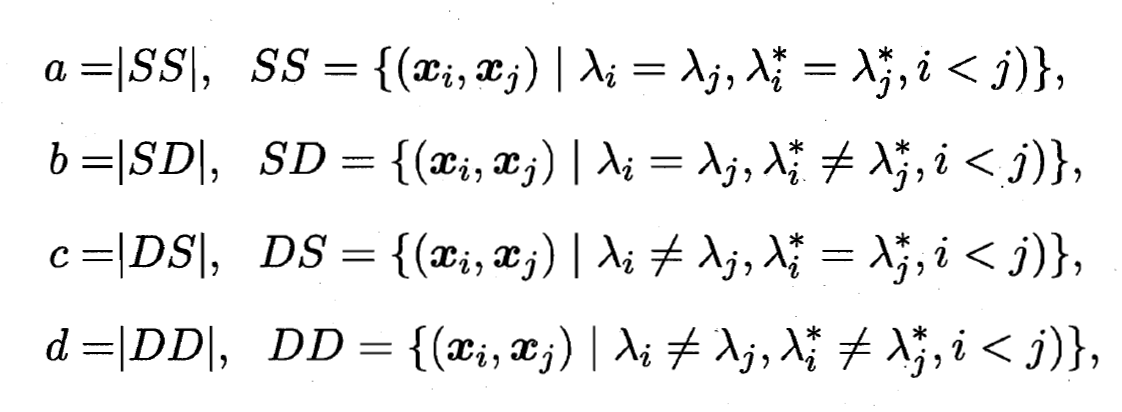
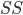 包含了在
包含了在 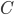 中隶属于相同簇且在
中隶属于相同簇且在 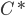 中也隶属于相同簇的样本对, 集合
中也隶属于相同簇的样本对, 集合 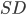 包含了在
包含了在 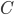 中隶属于相同簇但在
中隶属于相同簇但在 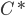 中隶属于不同簇的样本对, 由于每个样本对
中隶属于不同簇的样本对, 由于每个样本对 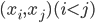 仅能出现在一个集合中, 因此有
仅能出现在一个集合中, 因此有 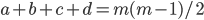 成立. 则有:
成立. 则有:

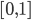 区间, 值越大越好. 考虑聚类结果的簇划分
区间, 值越大越好. 考虑聚类结果的簇划分 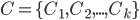 , 定义:
, 定义: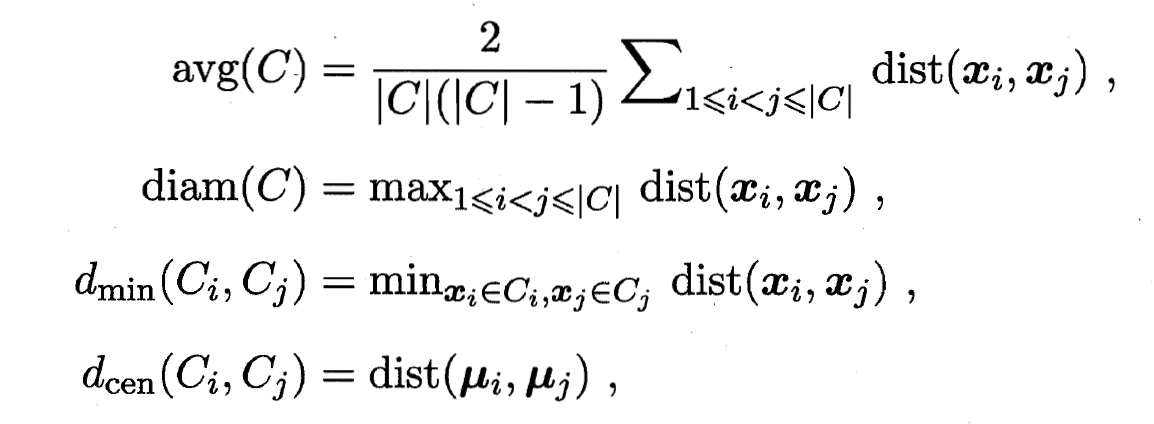
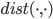 用于计算两个样本之间的距离;
用于计算两个样本之间的距离; 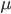 代表簇
代表簇 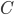 的中心点
的中心点 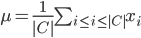 . 显然,
. 显然, 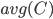 对应于簇
对应于簇 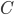 内样本间的平均距离,
内样本间的平均距离, 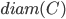 对应于簇
对应于簇 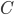 内样本间的最远距离,
内样本间的最远距离, 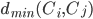 对应于簇
对应于簇 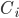 与簇
与簇 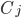 最近样本间的距离,
最近样本间的距离, 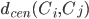 对应于簇
对应于簇 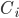 与簇
与簇 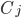 中心点检的距离, 则有:
中心点检的距离, 则有:
Be First to Comment