Press "Enter" to skip to content
写在前面
- 在这篇文章中, 我们继续学习线性判别分析与多分类学习小节中的内容. 本文中涉及到的数学问题与名词比较多, 数学不好的同学也不害怕, 先过一遍, 有个概念之后就知道如何去查找解决不懂的问题了. 后续笔者也会相应的补充一些数学类的文章更新上来, 学习有个过程, 不要害怕未知, 每天学一点, 积累下来, 久而久之, 回头一看, 会发现自己已经不是曾经那个自己, 早已走远.
线性判别分析
- 线性判别分析(Linear Discriminant Analysis, 简称LDA), 是一种经典的线性学习方法, 在二分类问题上因为最早由Fisher提出, 亦称'Fisher判别分析'. LDA的思想非常朴素: 给定训练样例集, 设法将样例投影到一条直线上, 使得同类样例的投影点极可能接近, 一类样例的投影点尽可能远离; 在对新样本进行分类时, 将其投影到同样的这条直线上, 在根据投影点的位置来确定新样本的类别. 如下图, ' ', '-'分别代表正例和反例, 椭圆表示数据簇的外轮廓, 虚线表示投影, 红色实心圆和实心三角形分别表示两类样本投影后的中心点:
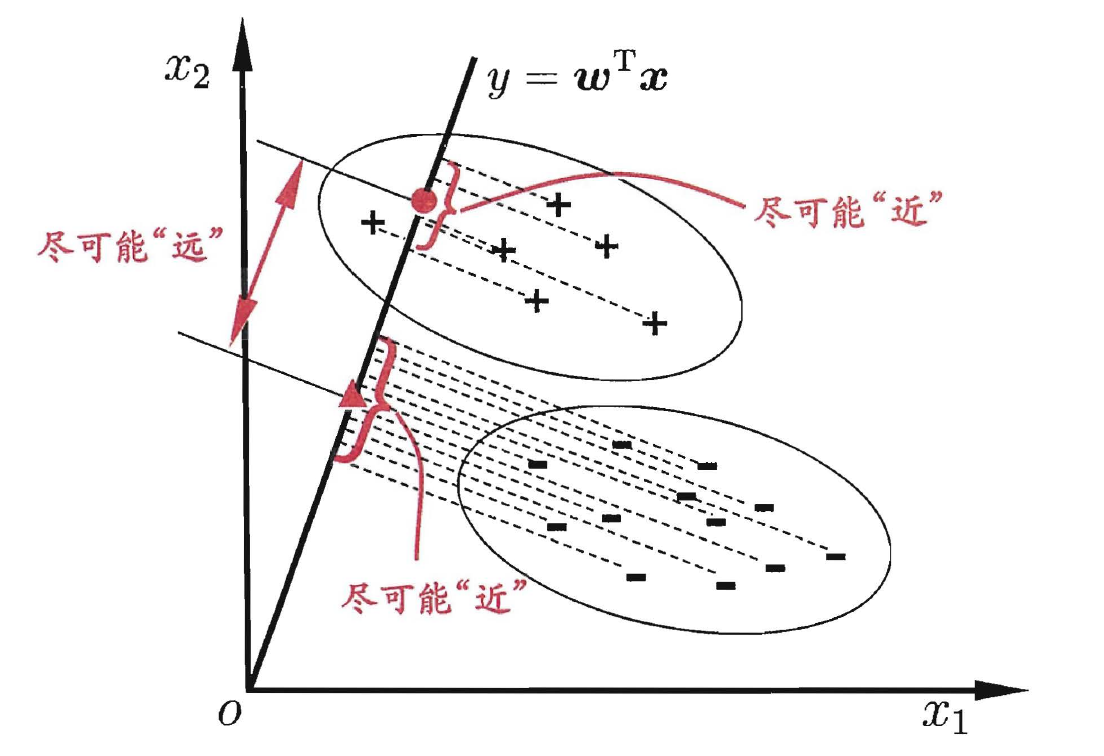
- 给定数据集
 ,
,  , 令
, 令  分别表示第
分别表示第 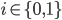 类示例的集合, 均值向量, 协方差矩阵. 若将数据投影到直线
类示例的集合, 均值向量, 协方差矩阵. 若将数据投影到直线 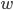 上, 则两类样本的中心在直线上的投影分别为
上, 则两类样本的中心在直线上的投影分别为  和
和  ; 若将所有样本点都投影到直线上, 则两类样本的协方差分别为
; 若将所有样本点都投影到直线上, 则两类样本的协方差分别为  和
和  . 由于直线是以为空间, 因此
. 由于直线是以为空间, 因此  ,
,  ,
,  和
和  均为实数.
均为实数.
- 欲使同类样例的头用电尽可能接近, 可以让同类样例投影点的协方差尽可能小, 即
 尽可能小; 而欲使一类样例的投影点极可能远离, 可以让类中信之间的距离尽可能大, 即
尽可能小; 而欲使一类样例的投影点极可能远离, 可以让类中信之间的距离尽可能大, 即  尽可能大. 同时考虑二者, 则可得到欲最大化的目标:
尽可能大. 同时考虑二者, 则可得到欲最大化的目标:

- 定义'类内三都矩阵'(Within-Class Scatter Matrix):


- 则有:

- 这就是LDA欲最大化的目标, 即
 与
与  的'广义瑞利商'(Generalized Rayleigh Quotient).
的'广义瑞利商'(Generalized Rayleigh Quotient).
- 令
 , 则有:
, 则有:


- 由拉格朗日乘子法, 上式等价于:

- 其中
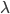 是拉格朗日乘子. 注意到
是拉格朗日乘子. 注意到  的方向恒为
的方向恒为  , 不妨令
, 不妨令  , 则有:
, 则有:

- 考虑到数值解的稳定性, 在实践中通常是对
 进行奇异值分解, 即
进行奇异值分解, 即  , 这里
, 这里  是一个实对角矩阵, 其对角线上的元素是
是一个实对角矩阵, 其对角线上的元素是  的奇异值, 然后再由
的奇异值, 然后再由  , 得到
, 得到  .
.
- LDA可以从贝叶斯决策理论的角度来阐述, 并可证明, 当两类数据同先验, 满足高斯分布且协方差相等时, LDA可达到最优分类. 可以将LDA推广到多分类任务中. 假定存在
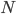 个类, 且第
个类, 且第 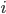 类示例数为
类示例数为 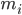 . 我们先定义'全局散度矩阵':
. 我们先定义'全局散度矩阵':


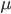 是所有示例的均值向量. 将类内散度矩阵
是所有示例的均值向量. 将类内散度矩阵  重定义为每个类别的散度矩阵之:
重定义为每个类别的散度矩阵之:

- 其中:

- 则可得:


- 多分类LDA可以有多种实现方法: 使用
 ,
,  ,
,  三者中的任何两个即可. 常见的一种实现是采用优化目标:
三者中的任何两个即可. 常见的一种实现是采用优化目标:

- 其中
 ,
,  表示矩阵的迹(Trace). 则可通过如下广义特征值问题求解:
表示矩阵的迹(Trace). 则可通过如下广义特征值问题求解:

 的闭式解则是
的闭式解则是  的
的  个最大广义特征值所对应的特征向量组成的矩阵. 若将
个最大广义特征值所对应的特征向量组成的矩阵. 若将  视为一个投影矩阵, 则多分类LDA将样本投影到
视为一个投影矩阵, 则多分类LDA将样本投影到  维空间,
维空间,  通常远小于数据原有的属性数. 于是, 可通过这个投影来减小样本点的维数, 且投影过程中使用了类别信息, 因此LDA也常被视为一种经典的监督降维技术.
通常远小于数据原有的属性数. 于是, 可通过这个投影来减小样本点的维数, 且投影过程中使用了类别信息, 因此LDA也常被视为一种经典的监督降维技术.
多分类学习
- 考虑
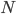 个类别
个类别  , 多分类学习的基本思路是'拆解法', 即将多分类任务拆分为若干个二分类任务求解. 最经典的拆分策略有三种: '一对一'(One vs. One, 简称OvO), '一对其余'(One vs. Rest, 简称OvR)和'多对多'(Many vs. Many, 简称MvM).
, 多分类学习的基本思路是'拆解法', 即将多分类任务拆分为若干个二分类任务求解. 最经典的拆分策略有三种: '一对一'(One vs. One, 简称OvO), '一对其余'(One vs. Rest, 简称OvR)和'多对多'(Many vs. Many, 简称MvM).
- 给定数据集
 ,
,  . OvO将这
. OvO将这 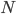 个类别两两配对, 从而产生
个类别两两配对, 从而产生  个二分类任务. 在测试阶段, 新样本将同时提交给所有分类器, 浴室我们将得到
个二分类任务. 在测试阶段, 新样本将同时提交给所有分类器, 浴室我们将得到  个分类结果, 最终结果可通过投票产生: 即把被预测得最多的类别作为最终分类结果. 如下图:
个分类结果, 最终结果可通过投票产生: 即把被预测得最多的类别作为最终分类结果. 如下图:
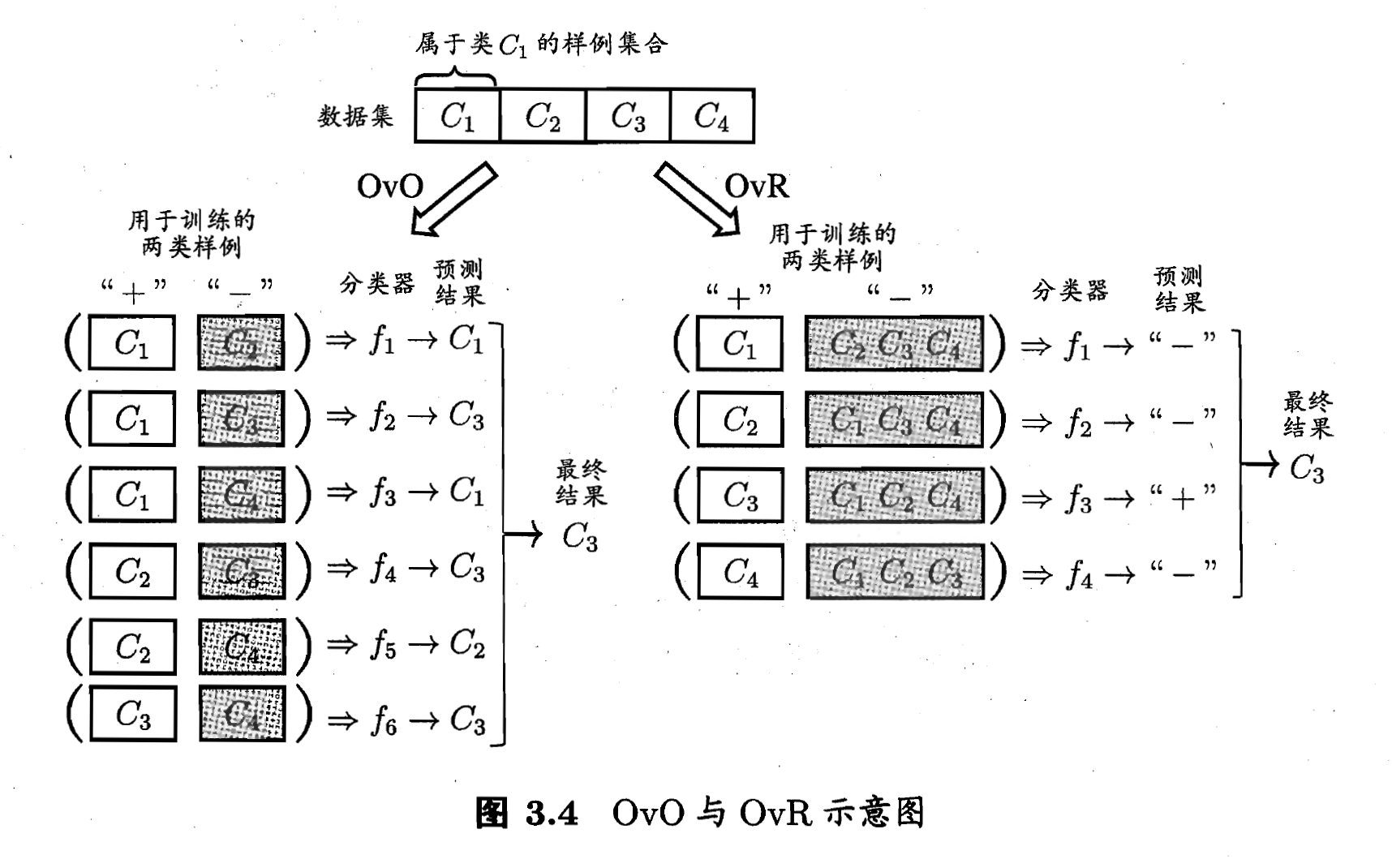
- MvM是每次将若干个类作为正类, 若干个其他类别作为反类. 显然, OvO和OvR是MvM的特例. MvM的正, 反类构造必须有特殊的设计, 不能随意选取.
- '纠错输出码'(Error Correcting Output Codes, 简称ECOC): ECOC是一种最常用的MvM技术, 主要是将编码的思想引入类别拆分, 并尽可能在解码过程中具有容错性. ECOC工作过程主要分为两步:
- 编码: 对
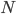 个类别做
个类别做  此划分, 每次划分将一部分类别划为正类, 一部分划分为反类, 从而星恒一个二分类训练集; 这样一共产生
此划分, 每次划分将一部分类别划为正类, 一部分划分为反类, 从而星恒一个二分类训练集; 这样一共产生  个训练集, 可训练出
个训练集, 可训练出  个分类器.
个分类器.
- 解码:
 个分类器分别对测试样本进行预测, 这些预测标记组成一个编码. 将这个预测编码与每个类别各自的编码进行比较, 返回其中距离最小的类别作为最终预测结果.
个分类器分别对测试样本进行预测, 这些预测标记组成一个编码. 将这个预测编码与每个类别各自的编码进行比较, 返回其中距离最小的类别作为最终预测结果.
- 类别划分通过'编码矩阵'(Coding Matrix)指定. 编码矩阵有多重形式, 常见的主要有二元码和三元码. 前者将每个类别分别指定为正类和反类, 后者在正, 反类之外, 还可以指定停用类, 如下图:

写在后面
- 本文看不懂没关系, 先大致有个了解, 慢慢深入, 贵在坚持.
- 明天, 我们将会继续学习类别不平衡问题.
Related

 ,
,  , 令
, 令  分别表示第
分别表示第 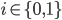 类示例的集合, 均值向量, 协方差矩阵. 若将数据投影到直线
类示例的集合, 均值向量, 协方差矩阵. 若将数据投影到直线 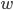 上, 则两类样本的中心在直线上的投影分别为
上, 则两类样本的中心在直线上的投影分别为  和
和  ; 若将所有样本点都投影到直线上, 则两类样本的协方差分别为
; 若将所有样本点都投影到直线上, 则两类样本的协方差分别为  和
和  . 由于直线是以为空间, 因此
. 由于直线是以为空间, 因此  ,
,  ,
,  和
和  均为实数.
均为实数. 尽可能小; 而欲使一类样例的投影点极可能远离, 可以让类中信之间的距离尽可能大, 即
尽可能小; 而欲使一类样例的投影点极可能远离, 可以让类中信之间的距离尽可能大, 即  尽可能大. 同时考虑二者, 则可得到欲最大化的目标:
尽可能大. 同时考虑二者, 则可得到欲最大化的目标:




 与
与  的'广义瑞利商'(Generalized Rayleigh Quotient).
的'广义瑞利商'(Generalized Rayleigh Quotient). , 则有:
, 则有:


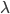 是拉格朗日乘子. 注意到
是拉格朗日乘子. 注意到  的方向恒为
的方向恒为  , 不妨令
, 不妨令  , 则有:
, 则有:
 进行奇异值分解, 即
进行奇异值分解, 即  , 这里
, 这里  是一个实对角矩阵, 其对角线上的元素是
是一个实对角矩阵, 其对角线上的元素是  的奇异值, 然后再由
的奇异值, 然后再由  , 得到
, 得到  .
.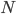 个类, 且第
个类, 且第 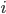 类示例数为
类示例数为 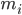 . 我们先定义'全局散度矩阵':
. 我们先定义'全局散度矩阵':

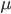 是所有示例的均值向量. 将类内散度矩阵
是所有示例的均值向量. 将类内散度矩阵  重定义为每个类别的散度矩阵之:
重定义为每个类别的散度矩阵之:



 ,
,  ,
,  三者中的任何两个即可. 常见的一种实现是采用优化目标:
三者中的任何两个即可. 常见的一种实现是采用优化目标:
 ,
,  表示矩阵的迹(Trace). 则可通过如下广义特征值问题求解:
表示矩阵的迹(Trace). 则可通过如下广义特征值问题求解:
 的闭式解则是
的闭式解则是  的
的  个最大广义特征值所对应的特征向量组成的矩阵. 若将
个最大广义特征值所对应的特征向量组成的矩阵. 若将  视为一个投影矩阵, 则多分类LDA将样本投影到
视为一个投影矩阵, 则多分类LDA将样本投影到  维空间,
维空间,  通常远小于数据原有的属性数. 于是, 可通过这个投影来减小样本点的维数, 且投影过程中使用了类别信息, 因此LDA也常被视为一种经典的监督降维技术.
通常远小于数据原有的属性数. 于是, 可通过这个投影来减小样本点的维数, 且投影过程中使用了类别信息, 因此LDA也常被视为一种经典的监督降维技术.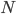 个类别
个类别  , 多分类学习的基本思路是'拆解法', 即将多分类任务拆分为若干个二分类任务求解. 最经典的拆分策略有三种: '一对一'(One vs. One, 简称OvO), '一对其余'(One vs. Rest, 简称OvR)和'多对多'(Many vs. Many, 简称MvM).
, 多分类学习的基本思路是'拆解法', 即将多分类任务拆分为若干个二分类任务求解. 最经典的拆分策略有三种: '一对一'(One vs. One, 简称OvO), '一对其余'(One vs. Rest, 简称OvR)和'多对多'(Many vs. Many, 简称MvM). ,
,  . OvO将这
. OvO将这 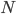 个类别两两配对, 从而产生
个类别两两配对, 从而产生  个二分类任务. 在测试阶段, 新样本将同时提交给所有分类器, 浴室我们将得到
个二分类任务. 在测试阶段, 新样本将同时提交给所有分类器, 浴室我们将得到  个分类结果, 最终结果可通过投票产生: 即把被预测得最多的类别作为最终分类结果. 如下图:
个分类结果, 最终结果可通过投票产生: 即把被预测得最多的类别作为最终分类结果. 如下图:
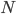 个类别做
个类别做  此划分, 每次划分将一部分类别划为正类, 一部分划分为反类, 从而星恒一个二分类训练集; 这样一共产生
此划分, 每次划分将一部分类别划为正类, 一部分划分为反类, 从而星恒一个二分类训练集; 这样一共产生  个训练集, 可训练出
个训练集, 可训练出  个分类器.
个分类器. 个分类器分别对测试样本进行预测, 这些预测标记组成一个编码. 将这个预测编码与每个类别各自的编码进行比较, 返回其中距离最小的类别作为最终预测结果.
个分类器分别对测试样本进行预测, 这些预测标记组成一个编码. 将这个预测编码与每个类别各自的编码进行比较, 返回其中距离最小的类别作为最终预测结果.
Be First to Comment