写在前面
- 在这个章节中, 我们主要来探讨如何针对组合函数求导, 其中包括, 函数相加, 函数相乘, 以及链式法则.
加法法则

- 如图, 我们想要对函数
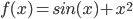 求导.
求导. - 假设
 , 则此处
, 则此处  . 假设在此处增长微量
. 假设在此处增长微量 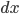 , 则增加的高度变化值为
, 则增加的高度变化值为  , 最后推导出
, 最后推导出  .
. - 加法法则:

乘法法则

- 如图, 我们要对函数
 求导.
求导. - 假设增长微量
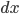 , 则增加的面积变化值为
, 则增加的面积变化值为  , 由于
, 由于  非常小, 这里可以将其忽略, 则有
非常小, 这里可以将其忽略, 则有  , 最后推导出
, 最后推导出 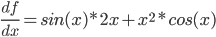 .
. - 乘法法则(左乘右导, 右乘左导):

链式法则

- 如图, 我们要对函数
 求导.
求导. - 最上面的x为x轴的值, 这个值会直接影响
 的结果,
的结果,  的结果会直接对
的结果会直接对  的结果造成影响.
的结果造成影响. - 我们假设x移动了一个微量dx, 这个dx对
 造成的影响为
造成的影响为  , 我们暂且将
, 我们暂且将  看做函数h, 则h对
看做函数h, 则h对  造成的影响为
造成的影响为  , 最后将
, 最后将 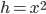 带入, 推导出
带入, 推导出  , 得出
, 得出 
- 在这里, 我们必须一提的链式法则来了:


写在最后
- 这章节中, 主要介绍了加法法则, 乘法法则, 链式法则以及其推导过程, 这些知识都是非常基础且重要的.
Be First to Comment